
THE
WHYS AND WHEREFORES
OF
NAVIGATION
BY
Navigating Officer and Senior Instructor New York State Nautical
Schoolship “Newport,” Late Nautical Expert,
Hydrographic Office, U. S. N.
ILLUSTRATED

NEW YORK
D. VAN NOSTRAND COMPANY
25 Park Place
1918
Copyright, 1918, by
D. VAN NOSTRAND COMPANY
PRESS OF
BRAUNWORTH & CO.
BOOK MANUFACTURERS
BROOKLYN, N. Y.
TO THE
AMERICAN SUB-PATROL
whose War Zone record of skill and daring
has the author’s profound respect
and admiration
[Pg vii]
When taking into consideration the number of excellent works now published on navigation there would seem to be a small chance of finding a different angle from which to discuss the subject. The purpose of the majority of such books is to give instruction to beginners. This book, however, is written particularly for the men who do their work mostly by rote and wish to know more of the reasons; or, perhaps, for schoolship graduates who may here find a chance to extend their horizons.
I have not considered it desirable to avoid repetition and in order to closely follow a line of thought have freely repeated many points already taken up. This has in a number of cases avoided the distraction of seeking a page of reference elsewhere.
I have had in mind that it serve as supplementary reading to the American Practical Navigator, Bowditch, that great bulwark of navigation which for over a hundred years has protected American ships through every deed of valor and every commercial adventure. It is placed beyond criticism by its venerable name and its remarkable record and, as a reference book for the navigator, it stands without a peer, but as a text book it founders the student.
If to such mariners as these a little insight is given to the “Whys and Wherefores” of their work, I shall be well repaid for the work of many watches below.
These discussions appeared several years ago, in a less extended form, in the Master, Mate and Pilot, the magazine formerly published by the American Association of Masters, Mates and Pilots.
I have freely consulted the following standard works: American Practical Navigator, Bowditch; Wrinkles in Practical Navigation, Lecky; The Theory and Practice of Navigation, Dunraven; General Astronomy, Young; Navigation and Compass Adjustment, Muir; Guide to the Marine Board’s Examinations, Reed.
I have received and am grateful for very valuable help and suggestions from Mr. George W. Littlehales, Hydrographic Engineer, U.S.N., Mr. Felix Riesenberg, C.E., Commander New York State Schoolship Newport, and George A. Collie (deceased), Nautical Expert, Hydrographic Office, U.S.N.
G. B.
New York, April 15, 1918.
CONTENTS
| PAGE | |
| CHAPTER I | |
| Introductory Remarks | 1 |
| CHAPTER II | |
| Nautical Astronomy | 5 |
| CHAPTER III | |
| Declination and Right Ascension, including Precession | 15 |
| CHAPTER IV | |
| Time | 33 |
| CHAPTER V | |
| Corrections for Observed Altitudes | 68 |
| CHAPTER VI | |
| Latitude | 78 |
| CHAPTER VII | |
| Azimuths and Amplitudes | 93 |
| CHAPTER VIII | |
| Longitude | 101 |
| CHAPTER IX | |
| Sumner Method, including New Navigation | 107 |
| CHAPTER X | |
| The Moon | 139 |
| CHAPTER XI | |
| Charts | 146 |
| Index | 161 |
THE WHYS AND WHEREFORES
OF NAVIGATION
In embarking upon the study of navigation familiarity with the compass is the first logical step: the quick mental conversion of a course or direction given in points to the same direction in degrees expressed in quadrants as S. 35° E., and again into a system by which direction is indicated by degrees from 0° to 360°. A mariner will encounter all three of these systems and will find constant conversion necessary back and forth for various purposes. The 0° to 360° system is the most up-to-date and the simplest form of handling direction.
Following the compass may be taken up the use and description of other nautical instruments with which every mariner is supposed to be familiar.
Dead reckoning is the first calculation to appear and this involves the correction of the compass courses back and forth between true, magnetic and compass directions. This is dealt with under Azimuths and Amplitudes. In practical navigation a vessel commences her voyage and [Pg 2] attempts to sail in a certain direction, but the well-known elements of compass error, variation and deviation, current, wind, seas and poor steering all divert the vessel from the projected course. In dead reckoning a navigator strives to keep track of his position by keeping a record of actual courses steered and distances run. He then is obliged to guess at the amount the vessel has diverted both in direction and distance until an astronomical observation sets him straight again. It is here particularly shown that navigation becomes an art of estimating position and the better the navigator’s bump of locality, the greater his success. This is a peculiar gift and usually is born in the man, at least it cannot be learned from books. The process of finding latitude and longitude by dead reckoning is supposed to be already well known to the reader and will not be detailed at length.
However, every course angle is laid off from a meridian (which is true N. and S.) and terminates in a parallel of latitude. This meridian and parallel intersect at right angles; hence these with the distance run (which is the hypothenuse) form a plane right angle triangle, plane because the curvature of the earth is not considered in short distances. To solve this triangle, we have the course angle and one side—the distance run. With these the other two sides are easily found by computation, but more easily by tables No. 1 and 2, Bowditch. The side along the meridian is represented by the column headed Lat. (difference of latitude) and the side lying in the parallel is in the column headed Dep. (departure). Thus the values of the sides of the triangle are given in miles and tenths, showing the distance good made N. or S. and E. or W.
[Pg 3] It will be noted that at the top of the pages of these tables are four different courses and at the bottom are likewise four courses making the same page serve for eight different courses. This is accomplished by the fact that triangles formed by these particular eight courses are the same in shape. Thus N. 30° E., for instance, makes a similar triangle to N. 30° W. (330°); S. 30° E. (150°); or S. 30° W. (210°). They have identically the same difference of latitude and departure. If this fact is not clear draw a diagram and be convinced. In the cases of N. 60° E. (60°); N. 60° W. (300°); S. 60° E. (120°); S. 60° W. (240°), the same shaped triangle as above is found, but reversed in that what was the difference of latitude side now has become the departure side. The values of these sides are read from the bottom of the page and are found in the reverse columns to fit the reverse triangle. The latitude value read from the top of the page as 30° becomes a departure value when read from the bottom with 60°.
The subject of Sailings is one of the early problems confronting the student of navigation and will be considered briefly. The above remarks on dead reckoning cover the principle of plane sailing, the simple method where the spherical surface of the earth is ignored and a flat ocean substituted. This method will not serve for anything but short distances of a few hundred miles without sufficient error to render it impracticable. Traverse sailing is a series of plane sailing courses made, for instance, by a sailing vessel beating to windward.
In parallel sailing the vessel pursues a true E. or W. course and runs along a parallel of latitude. Thus all her [Pg 4] progress is in the terms of departure with no difference of latitude. As all meridians converge from the equator towards the poles the length in miles of a degree of longitude keeps on diminishing as the poles are approached and, conversely, miles of departure have an increasing value in degrees of longitude. So in parallel sailing what we desire to know is what is the value in the particular latitude of our course of our departure (miles) in ° ´ ´´ of longitude. Having this and applying it to the longitude left will give the longitude in. Middle latitude sailing is very similar to parallel sailing in that it is assumed, for the purpose of getting the difference of longitude, that the whole departure of the course or courses sailed has been made in the mean or middle latitude, because the greater value (in the northern hemisphere) in difference of longitude of a mile northward of the middle latitude is counteracted by the corresponding lesser value southward of the middle latitude.
Mercator sailing is perhaps the most extensively used, as the Mercator principle is employed almost universally in the construction of navigational charts. It is described under Charts in this book.
Also under Charts is a description of the Gnomonic Chart which is also called the Great Circle Chart and used in Great Circle Sailing, also referred to in those pages.
The young navigator is counselled never to know where his vessel is, lest through over confidence he be led into close and dangerous quarters.
The sun is the center of the solar system, with all the planets, including the earth, revolving around it, some with orbits greater and others less than that of the earth. The planets in some instances have satellites revolving in turn around them, as the moon in the case of the earth.
The movements of the earth will be, perhaps, more readily understood by assuming a position at the North Pole; here beneath the observer the earth is rotating left-handed—against the hands of a watch, once each day; while at the same time it is speeding onward through space in a left-handed curve, which in the course of a year resolves itself into a complete revolution around the sun.
The sun and stars are considered to be stationary for all navigational purposes, the apparent movements of these bodies being entirely due to the motions of the earth. The result of our daily rotation from west to east is, that the heavenly bodies march past our meridian in a majestic procession for 24 hours, after which the performance is repeated. The uninitiated are here forewarned against becoming confused by the assumption used for convenience by navigators that the heavens revolve around the earth.
[Pg 6] The planets and moon join the sun and stars in the daily parade past our meridian, but their apparent movements are not entirely an illusion, for they have motions of their own that somewhat affect the precision of their daily revolution. This is readily observed in the moon’s hour of rising, which is very perceptibly later each evening. Her actual revolution around the earth, being from west to east, is contrary to the apparent diurnal motion and thereby each evening finds her farther to the eastward and consequently rising later. As a result of this change in the time of rising, the moon must of necessity rise in every hour of both day and night in the course of a month—the time she requires to revolve around the earth.
The onward movement of the earth in its orbit as we face the sun in latitudes north of the tropics, is toward our right, and this causes the sun to apparently move slowly eastward or to the left among the stars, corresponding exactly to our movement westward. This movement is opposite to his daily course across the heavens. As a year is required for the earth to accomplish our revolution around the sun, it follows that this same length of time is consumed by the sun in making its apparent eastward revolution of the heavens.
The movements of the planets are more complex. They all revolve around the sun in the same direction as the earth, but as their orbits are of vastly different sizes, they will be found in various positions relative to the sun; they overhaul and pass each other, but owing to their uniform direction of revolution they never meet. The planetary system is like the horse race at a county [Pg 7] fair; the pole horse has the advantage, but the varying speeds of the contestants soon place them at various parts of the track.
From the earth the movements of the planets, aside from the diurnal movement, are composed of their own actual movement around the sun, combined with an apparent motion, due to the earth’s onward movement precisely as described above in the case of the sun. The combined movement of a planet may be noted by reference to the fixed stars beyond it.
The positions of heavenly bodies are determined by two measurements—coordinates—the distance north or south of the celestial equator, called the declination, and the distance east from the prime celestial meridian taken as a reference, called the right ascension, each of which will be subsequently treated at length under its individual heading. The movement of the planets eastward or westward as described, constantly changes their right ascension; and as their orbits are inclined at different angles to the celestial equator, they are always changing their declination.
The planets whose orbits are smaller than that of the earth are called inferior, while those whose orbits are of greater dimensions are known as superior planets. Mercury and Venus are inferior planets and consequently are always nearer the sun; their comparatively close proximity making them appear to us as morning and evening stars. In fact, Mercury is so close that it is unavailable, owing to the brilliancy of the sun, for observation with a sextant; while Venus, on the other hand, a little more remote, is an excellent body to observe, and is [Pg 8] always found in the east or west, conveniently near the prime vertical, the most favorable place for a time sight for longitude. The twilight or dawn which usually prevails at the time of a Venus sight gives the navigator a good horizon to observe upon. Mars, Jupiter and Saturn are superior planets and their travels are so extended that they may be found almost anywhere in the heavens within the limits of their declinations.
The earth’s orbit is slightly elliptical, with the sun located a little out of center—a little nearer one end. Should a line or axis be drawn through the long diameter, its intersection with that part of the orbit nearest the sun is called the Perihelion while the opposite point is known as the Aphelion. The former is used as a point of reference from which the earth’s position can be located in terms of angular measurement from time to time. This angle, known as the anomaly, is formed by the line from the sun to the Perihelion and that drawn from the sun to the earth. The latter distance is called the radius vector of the earth. We (the earth), are at the Perihelion about January 1, and consequently this angle at that date is 0°, but from this time on, the angle increases approximately one degree a day throughout the year.
The plane of the earth’s equator makes at all times an angle of about 23° 28´ with the plane of its orbit. This is a highly important angle to mankind, for upon it depends the climate of the world. The axis of the earth, if we can conceive it as represented by a slender imaginary staff, extends through the unlimited distance to a point in the heavens—the celestial pole; this point is in the zenith for a person at our north pole. Since the distance between [Pg 9] these points is mathematically infinite, any number of lines parallel to this “staff” will appear to penetrate the sky at the single point of the celestial pole. Thus the parallel positions of the axis corresponding to the earth’s various positions, even those at opposite sides of the orbit, converge into this common point. To be clearer, the parallel lines representing the different positions of the axis during the year according to our geometry form a group of separate points on the heavens, but the distance being beyond all reckoning, our limited conceptions fail to identify the group of points and it resolves into one point.
By the same line of reasoning the plane of the earth’s equator remains parallel in all its positions throughout the yearly cruise around the sun, and its projection marks but one celestial equator upon the sky.
While the direction of the axis and corresponding position of the equator are constant for all practical purposes, there is, nevertheless, an extremely slow circular movement of the axis, called the precession of the equinoxes, a subject which is reserved for subsequent discussion.
Coordinates
In nautical astronomy the earth is assumed to be the center of space with the heavens forming a globular shell around it, known as the celestial sphere. All fixed stars are assumed to lie on its concave surface from the earth regardless of their actual distances. The tracks of all other bodies moving, or appearing to move, across the sky are considered to be on the surface of this sphere.
[Pg 10] It is necessary, in order to conveniently define the position of heavenly bodies to mark this celestial sphere with imaginary circles to serve as coordinates, as we mark the earth with meridians of longitude and parallels of latitude.
Before going into the explanation of these coordinates, it may be well to consider a few facts concerning circles. A great circle is of course understood to be one whose plane passes through the center of a sphere, dividing it into two equal parts. There can be an infinite number of these circles whose planes cut the sphere at every possible inclination as long as they pass through its center. A circle may be a great circle of either the celestial sphere, the earth, or even of a baseball. The poles of a great circle are the points on the surface of its sphere, penetrated by the diameter perpendicular to the plane of the great circle. As for example, the poles of the earth are connected by the diameter that is perpendicular to the plane of the equator. An angle at any pole is measured on the great circle which subtends it. For instance, angles at the poles of the earth are measured on the equator; angles at the zenith on the horizon. With these facts well in mind we will proceed, showing the scheme of circles employed in laying off the surface of the heavens.
There are three systems of circles, each designed to fulfil a different requirement.
The first system depends upon the position of the observer and changes its whole imaginary structure to correspond with his movements. The plumb-line, if extended to the heavens overhead, will determine the zenith, the point of origin of this system on the celestial sphere. [Pg 11] The corresponding point directly beneath us is known as the nadir.
The great circle of the celestial sphere everywhere equally distant from both the zenith and the nadir is the horizon. It is plain that a new zenith and new horizon are created with every movement of the observer. The facts that man is on the surface and not at the center of the earth, and that his eye is elevated above its surface, each creates another horizon.
The rational horizon is marked by a plane, perpendicular to a plumb-line and passing through the earth’s center; while the sensible horizon is determined by a plane, also perpendicular to the plumb-line, but passing through the eye of the observer. It will therefore be seen that these two parallel horizons are some 4000 miles apart, the semi-diameter of the earth; but this distance when projected on the celestial sphere becomes insignificant when compared with the infinite distance of this sphere from the earth, and the rational and sensible horizons shrink into a single line so far as we can perceive.
While this statement is true when dealing with the stars, it needs modifying when dealing with the sun and moon, and in very accurate observations of planets, as their distances are insufficient to eliminate the angle formed between the line from the body to the center of the earth, and that from the body to the observer. This is allowed for when observing these bodies by applying the correction of parallax to the observed altitude.
The visible horizon is the boundary seen between the sea and sky. If the observer’s eye were at the level of [Pg 12] the sea, his visible horizon would coincide with the sensible horizon, defined above; but the elevation above the surface from which sights are taken causes the line of vision, tangent to the sea, to be depressed below the plane of the sensible horizon making an angle with it called the dip of the horizon. In practice all altitudes of heavenly bodies taken from a vessel are measured to the visible horizon and corrected for the dip to reduce them to the sensible horizon, then again corrected for parallax to obtain the true altitude of the body above the rational horizon; or what is the same thing, the altitude as observed at the center of the earth.
From the zenith, an infinite number of great circles, known as vertical circles, sweep around the celestial sphere, cutting the horizon at right angles and passing through the nadir. The one which cuts the north and south points is called the celestial meridian, and is evidently a projection of the terrestrial meridian. The vertical circle passing through the east and west points is called the prime vertical, and has a distinction above other vertical circles by virtue of its being the most favorable position for a body in observations for longitude. The heavens are further swept by an infinite number of parallels of altitude which are, as their name implies, parallel to the horizon.
The azimuth of a body is its angular distance from the north or south points of the horizon, determined by the angle formed at the zenith, or by the arc of the horizon between the meridian of the observer and the vertical circle passing through the body. Amplitude is the angle at the zenith formed by the prime vertical and the [Pg 13] vertical circle passing through the body or it is the angular distance from the east or west points, measured on the horizon, and is measured similarly to the azimuth.
The system of laying off the heavens just described is well enough for the momentary locating of a body, which is a very important feature in navigation, but for some purposes a more stable point than the zenith, which on shipboard is ever changing, is needed, from which to form a system that is constant the world over. To meet this demand we take the point in the sky penetrated by the prolongation of the earth’s northern axis—the celestial pole—and from this point meridians and parallels are developed upon the celestial sphere as has been done on the earth. In fact, it is as though these terrestrial coordinates were projected to the heavens where they hold the same relative positions as upon the earth. The northern celestial pole is in the zenith at our north pole. The same is true of the south pole. The celestial equator, or equinoctial, is a great circle, which is midway between the poles and everywhere 90° from them. It marks the termination of the plane of our equator extended to the celestial sphere, or in other words, it is always directly over our equator.
The parallels of the celestial sphere evolved by this system, corresponding to those of latitude upon the earth are called parallels of declination, while the celestial meridians having as their point of origin the prolongation of the earth’s axis, are known as hour circles. The particular hour circle passing through the zenith is one and the same with the celestial meridian. It will be seen that this circle must pass through the zenith, nadir and the poles.
[Pg 14] The angle formed at the pole by the hour circle passing through a body and a local meridian is the hour angle of that body, and is measured westward through 24 hours, although A.M. hour angles of the sun are reckoned eastward through 12 hours.
At the north pole where the zenith is identical with the celestial pole, the vertical circles, parallels of altitude and rational horizon are coincident with the hour circles, parallels of declination and the equator, respectively; but departing from this point they form angles with each other corresponding to the degrees of latitude from the pole; at the equator the angle reaches 90°.
The system of circles described above is by far the most extensively used, and positions determined by its coordinates are comparatively constant, but there is still a third system of circles which was used and handed down to us by the ancients. In the place of the celestial equator, a similar great circle is used, known as the ecliptic. This circle is determined by the extension of the plane of the earth’s orbit to the celestial sphere. The poles of the ecliptic everywhere 90° from this circle are the points from which meridians depart as upon the earth. The prime meridian of this system passes through the intersection of the celestial equator, and the ecliptic—the vernal equinox or First Point of Aries. Celestial latitude and longitude are the coordinates used with this system, but navigators universally prefer to use the well-known declination and right ascension. Hence the path of usefulness of the former seldom leads beyond the observatories.
Owing to the important place that declination holds in nautical astronomy, a detailed explanation will appropriately follow closely in the wake of the preceding remarks. It must be made clear, before getting under way, that declination is the distance, in degrees, minutes and seconds, of a body north (+) or south (-) of the celestial equator measured on the hour circle passing through the body. This distance is identical with the latitude of the place in the zenith of which the body happens to be. What declination is to a body in the heavens, latitude is to the place on the earth directly beneath it.
The declination of fixed stars changes very slowly from month to month, but the planets meander about on the celestial sphere in a way that is liable to puzzle anyone other than an astronomer. This element, however, is worked out in the observatory and given in the nautical almanac in a way that relieves the navigator of worry concerning the complex movements of these latter bodies. The same may be said of the moon, but the subject will be treated, somewhat superficially though sufficiently for the needs and desires of the practical mariner, in a special talk on the moon. This eliminates all the celestial bodies except the sun, the most important; and for this [Pg 16] reason the facts relative to its declination will be considered at some length.
As has already been stated, the sun is stationary, but our movements around it to the right causes it to appear to move to the left; precisely as you see, when under way, an anchored vessel’s masts move to the left along the land behind her, while you move on to the right. We have no landmarks behind the sun by which to observe his apparent movements, so in lieu of such ranges, we resort to the fixed stars, which serve as excellent marks to get a bearing on Old Sol and keep tab on him as he moves eastward among them. This movement must in no way be confounded with his apparent daily motion westward. As an illustration, we may see Orion—a familiar friend—swinging high in the western sky in the early evening; some weeks later he is riding low, and yet a little later still, he is swallowed up in the brilliancy of the setting sun. In other words, the sun and Orion have approached and passed each other. We know Orion does not move, for he is composed of fixed stars, and this seeming westward movement of his is in reality the apparent eastward marching of the sun, which is due to the earth’s movement of revolution. The sun in this apparent movement eastward follows a course at a rate equal to that of the earth, along a great circle of the celestial sphere called the ecliptic, a circle that plays an important part in the explanation of declination, particularly that of the sun. The ecliptic is marked by the extension of the earth’s orbit to the celestial sphere.
A few more words concerning great circles will be introduced here, and the following statements, while they apply [Pg 17] to great circles in general, especially fit the relationship of the equinoctial or celestial equator to the ecliptic. These two great circles cut each other at an angle of 23° 28´. Great circles always bisect each other, and hence any two great circles of the celestial sphere, regardless of the angle they may take with the celestial equator, must intersect each other at exactly opposite points, 180° apart. What is true in this regard of the celestial sphere is equally true of the great circles of the earth. A vertex of a great circle is the point which departs the greatest distance from the equator—the highest point of the circle reached in declination. There are two vertices 180° apart with the two points of intersection 90° in either direction. The declination or latitude of either vertex is equal to the angle at which the circles intersect each other. The intersections are called the equinoxes, and it may be well to say here that the word equinox has several meanings in navigation, often rendering it necessary to judge by the text which is intended. The vernal equinox, for instance, refers to a certain time of year—March 21st. The sun is that day directly overhead at the intersection of the equator and the terrestrial ecliptic and this point is sometimes called the vernal equinox. Again, the sun at the same time occupies a point on the heavens also known as the vernal equinox, which is at the intersection of the celestial equator and the ecliptic. The point in the orbit occupied by the earth at this time is also spoken of as the vernal equinox.
The reader is now asked to arouse his imagination and if possible to conceive himself a passenger in an aeroplane equipped with some remarkable power capable [Pg 18] of carrying him to a position in space, above, yet a little outside, the earth’s orbit, near the Perihelion, and there to heave to and view awhile an astronomical picture. Spread out before his unrestricted vision will be the earth, its orbit, and the sun. It is to be hoped that the imagination of the reader is still sufficiently supple to suppose the plane of the orbit to be the surface of an infinite ocean stretching away beyond human conception of distance and “breaking” against the celestial sphere; the “surfline” there marks the ecliptic; the “ocean’s” surface representing the great plane of the ecliptic. The sun will be seen as if at anchor in his proper place within the orbit. The earth is “underway,” half submerged, and listed 23° 28´ toward our point of vantage. This inclination, or direction of the axis, is in a general way toward the perihelion, and within a few degrees of being parallel with the long diameter of the orbit. The earth maintains this nearly parallel position of its axis with the long diameter throughout the period of its revolution; a fact of importance to remember.
It will be readily seen that during the encircling of the sun there must be one position where the northern axis is inclined directly toward that body, another opposite where it is headed away from him, and two positions midway where the bearing of the axis (projected on the plane of the orbit) is at right angles to the bearing of the sun from the earth; another feature to be “salted down” in the memory.
If the earth revolved on an even keel, the equator and the “waterline” would be coincident, but fortunately this is not the case, and owing to the inclination of the axis [Pg 19] another great circle is defined by the “waterline,” called the terrestrial ecliptic, being directly beneath its celestial namesake. The inclination of the northern pole being in a general way toward the perihelion, correspondingly depresses or “submerges” that half of the equator below the plane of the ecliptic, represented by the “water surface,” and at the same time the opposite side rolls the equator above it. At two points (the equinoxes) on opposite sides of the earth, and at right angles to the direction of its inclination, the equator and terrestrial ecliptic cross each other at the “water’s edge.”
The sun is always exactly overhead for that point of the earth which is nearest to it. This is an essential fact to remember in navigation. Bearing in mind that the sun is stationary and ignoring for a time the rotation of the earth, each advance in its orbit brings about a change of bearing of the sun and a new position becomes the nearest point, and thereby directly beneath the sun. The constant changing of the sun’s bearing continues throughout the year, or one revolution, and a circle of these overhead positions is marked upon the earth, which is coincident with the terrestrial ecliptic—the visionary “waterline.” It is obvious that the vertical rays of the sun must apparently follow this line, for it can only be overhead for places that are in the same plane, and this again is the level of the “ocean.”
This circle of overhead positions projected on the celestial sphere marks the ecliptic—the “margin” of the infinite ocean, and the path that the sun seems to follow eastward among the stars.
The above paragraphs show us that the sun in following [Pg 20] this line around the earth crosses the equator twice, and twice he attains a distance of 23° 28´ from it, and so must be on the equator twice and reach a declination of 23° 28´ north and 23° 28´ south in the course of one year.
Returning to our imaginary illustration, we will now follow the peregrinations of the earth for a year and note the effect of its inclination in the different parts of the orbit upon the declination of the sun.
It will be assumed that it is the 21st of March and from our airy position we see the earth away on our right nearly 90° from the Perihelion. As this is the vernal equinox, there are a number of interesting points to be considered: The direction of the earth’s axis, projected on the plane of the orbit, is at right angles to the bearing of the sun from the earth; the sun is directly over the intersection of the equator and terrestrial ecliptic, and being overhead for this point on the equator, the declination must be 0°. Moreover, a line drawn from this intersection, or terrestrial vernal equinox, through the center of the sun and extended to the celestial sphere would strike the corresponding intersection of the ecliptic and the equinoctial or celestial equator—the celestial vernal equinox. The arrival of the earth at this position is the signal of spring for the northern hemisphere, likewise it announces the advent of autumn to our southern neighbors below the “Line.” The sun this day rises in the east (approximately) and passing through the zenith, sets in the west for those living on the equator. The explorer at the north pole is cheered by the first light as the sun appears in the horizon, while the south pole becomes enshrouded in the long Antarctic night. Without lingering [Pg 21] for ceremonies over the change of seasons, the earth continues steadily on its way toward the aphelion; the sun’s vertical rays leave the intersection of the equator and the terrestrial ecliptic, and follow along the latter, thus widening its distance from the equator as the earth proceeds. As the ecliptic in this half of the orbit is above, or north, of the equator the former is in north latitude and the sun, following along it, is thereby also in north declination. A line from any place having the vertical rays, through the sun to the celestial sphere, always terminates on the celestial ecliptic, all being in the same plane, and shows the corresponding celestial position of the sun on it. Its declination distance from the celestial equator, in degrees, minutes and seconds, is identical with that of the place on the earth directly beneath it relative to our equator. So by showing the course of the sun’s overhead positions on the earth its celestial positions are, at the same time, indicated. The overhead position of the sun on the terrestrial ecliptic gradually departs from the equator culminating about June 21st, the summer solstice, in a declination of 23° 28´ at a point near the aphelion in the orbit, 90° (approximately) from the equinox.
The positions in the orbit of the summer and winter solstices are reached by the earth several days before the points of the aphelion and perihelion. These respective positions would be in conjunction were it not for a slow and remarkable motion of the earth’s axis before spoken of, and later to be described, called the precession of the equinoxes.
The summer solstice is the great half-way point of the earth’s annual circumnavigation of the sun; it is a matter [Pg 22] of moment all over the world, and another great change of seasons is at hand. The sun is overhead for places along the parallel of 23° 28´ N. and bears north 23° 28´ from the zenith at noon from places on the equator.
At the north pole, since its appearance on the horizon on March 21st, the sun has mounted to an altitude of 23° 28´ and to nearly 67° at places on the Arctic circle. The earth’s northern axis is, in this position, inclined 23° 28´ directly toward the sun, which pours its rays continuously upon the northern regions, uninterrupted even by the earth’s daily rotation. It is on this day that the whole Arctic zone enjoys the full glory of the midnight sun. The earth’s continuous movement of revolution does not allow a delay of this favorable season in northern latitudes, but continues to make the sun’s vertical rays follow the terrestrial ecliptic as before on its way toward the intersection with the equator 90° away. On this leg of the journey, the sun is traveling on the upper one of two converging lines and thereby gradually lessening its distance from the other—the equator—or, in other words, reducing its declination. This continues until September 21st when the autumnal equinox is reached and the sun’s declination becomes 0°. The sun now being overhead at the intersection of the equator and the terrestrial ecliptic, is on the opposite side of the earth from the intersection of March 21st. In fact the conditions are similar, but now the earth is on the opposite side of the sun, and the change of seasons is the entrance of spring for the dwellers in southern latitudes.
The sun has dropped lower and lower in the sky at the north pole since June, until on this day it is in the [Pg 23] horizon and it is time for the Esquimos to seek their igloos and prepare to hibernate during the long Arctic night now ushered in.
The sunshine at the time of the equinoxes is equally distributed over the northern and southern zones, and the zenith distance of the sun at noon at any place is, theoretically, equal to the latitude of the place (except a small error due to change of declination accumulated subsequent, or previous, to the instant of the equinox).
The conditions during the next six months are reversed as the earth proceeds into that half of the orbit containing the perihelion. Now the sun following the terrestrial ecliptic enters southern latitudes or south declination, for in this part of the orbit the equator is above (or north) the plane of the ecliptic. The sun’s diverging course from the equator leads it farther and farther southward until on or about December 21st it arrives at the winter solstice with a culmination of 23° 28´ south declination. At this point the earth is but a few degrees from the perihelion as it was from the aphelion at the summer solstice.
The earth’s north pole is now inclined directly away from the sun and its rays have entirely forsaken the Arctic for the Antarctic zone; notwithstanding the earth’s daily rotation, which brings alternating light and darkness to the greater part of the world, the northern polar regions are in a continuous shadow, and no sunlight reaches these remote parts. At this time of the year the northern hemisphere above the tropic of Cancer, is in an unfavorable position relative to the sun, and as a result places situated on parallels less remote than the Arctic are having long [Pg 24] nights and short days in proportion to their latitude north. On the other hand, in the southern hemisphere the days are longer and the nights shorter, as the southern latitude increases until at the Antarctic circle night disappears and the sunshine is uninterrupted. It is seen that this is an exact reversal of the conditions at the summer solstice.
The earth enters the last quadrant of the great ellipse of its orbit, the sun now approaches the equator as the earth nears the vernal equinox. The south declination diminishes until on March 21st it becomes 0° and the earth has completed its revolution. We will now go on another tack and instead of considering only the effects of declination due to the earth’s revolution, will assume that the earth has been halted in its onward course of revolution and is making its daily rotation in the same position. The earth turning from west to east causes the sun to appear to proceed from east to west in its diurnal motion. Each rotation, requiring 24 hours, marks upon the earth a circle of overhead positions parallel to the equator and hence without change of declination. The result of such a remarkable condition would be, no change of seasons and no change in the length of the days and nights. In reality, however, we are saved from such monotony, for both the motion of rotation and revolution of the earth are acting together and giving a compound effect on the apparent movements of the sun. This alters the daily circles just mentioned to a fine spiral of overhead positions, ever changing in declination. The daily difference of the sun’s declination shown in the Nautical Almanac is equivalent to the distance between two threads of this spiral.
[Pg 25] The change of declination is most directly seen and felt in the polar regions, where the activities of the denizens are mostly limited to the favorable phases of this change. At the north pole, after the sun has appeared above the horizon, this spiral of declination can be continuously followed. The sextant will disclose a constant increase in altitude as the sun circles round and round the sky, winding itself up and finally culminating at 23° 28´. The process is then immediately reversed. The stars here make daily circles of equal altitudes as their change of declination is insignificant; but the circles of the planets and the moon are converted into spirals, the fineness of which is in proportion to the rate of their change of declination.
The fact that the sun reaches an altitude of 23° 28´ at the pole at the summer solstice with its declination of a like amount and that on March 21st, when the sun is in the horizon with the altitude 0°, it is directly over the equator with 0° declination, shows that at this place (the pole) the altitude is equal to the declination. Should an explorer travel southward 1°, his sextant would show an altitude 1° greater than at the pole, yet moving about does not affect the declination at a given time. It follows by taking his altitude at noon the explorer in the polar regions may readily learn his distance from the pole by subtracting the declination in the Nautical Almanac from his sextant reading.
It may not generally be known that the southern summer is shorter than the summer of the northern hemisphere, but such is the case by approximately eight days. The reason of this inequality lies in the fact that the sun [Pg 26] is nearer one end of the orbital ellipse, and the short diameter passing through this body divides the orbit into unequal parts. The smaller part being that traveled by the earth during the southern summer. Furthermore the nearer proximity of the sun causes an accelerated motion which further tends to lessen the time spent by the earth in this part of the orbit.
Right Ascension
Declination and right ascension being used together as coordinates, we will not separate them. It will be remembered that the equator and the terrestrial ecliptic cross each other on opposite sides of the earth; that on or about March 21, the sun is overhead at the intersection that is the vernal equinox. Now if at this intersection on this day a plumb-line were carried upward, it would at length reach the sun, and continued to infinity and projected on the celestial sphere would locate a point called the celestial vernal equinox, known by many as the First Point of Aries. This point is one of the most important celestial “landmarks” used in astronomy and navigation, but, unfortunately, no heavenly body marks its place. However, as its relative position among the neighboring stars is well known, its exact location is easily ascertained.
The hour circle which passes through this point is known as the equinoctial colure, and may be considered the prime meridian of the heavens, for from it is measured the right ascension of all bodies. Right ascension of a body is the angle at the celestial pole between this meridian of reference and the hour circle passing through [Pg 27] the body. It is always measured eastward through 24 hours of sidereal time (360°). The angle is measured by the arc intercepted on the celestial equator. For example, a star 15° east of the equinoctial colure has a right ascension of 1 hour or 15°, but, if the star is 15° west, its right ascension is 23 hours or 345°.
The positions of heavenly bodies are defined by right ascension and declination exactly as positions upon the earth are expressed by longitude and latitude, right ascension corresponding to longitude and declination to latitude.
In the discussion of Time, to follow, more facts concerning right ascension will be found.
Precession of the Equinoxes
A comparison of the present positions of the fixed stars with their places as recorded in ancient times shows a great discrepancy. The celestial latitudes, which were reckoned from the ecliptic, show no appreciable change; but in the declinations and right ascensions there is a great departure from the old positions. The error of right ascension was found by the old Greek astronomer, Hipparchus, to appear as a uniform eastward movement of all the stars, which led him to reason that, instead of the stars themselves changing, their point of reference was moving westward, thus lengthening all right ascensions.
The famous astronomer after further reasoning decided that the position of the celestial pole was changing, in fact that the line of the earth’s axis was describing a circle on the heavens, which was left-handed or against the hands of a watch as viewed from the north pole of [Pg 28] the earth. This movement was found to be extremely slow, requiring 25,800 years to complete the circle which has as its radius the amount of the inclination of the earth’s axis—23° 28´.
If a match is put through a piece of cardboard about the size of a half dollar to the distance of ¼ inch, and spun, the motion of the cardboard just as it staggers through loss of speed, gives some idea, although exaggerated, of the precession movement of the plane of the equator, which is of course infinitely slower. The movement of the top of the match is a semblance of the corresponding motion of the vanishing point of the axis on the celestial sphere.
The earth, as already explained, points its axis at practically the same spot in the heavens throughout the year, and if it were not for this annual precession of 50´´ it would for all intents and purposes hold a permanent direction. About December 21, the winter solstice, while the earth is still some degrees from the perihelion, its northern axis, is inclined directly away from the sun. Each year this distance from the perihelion is becoming greater, widening this angle between the direction of the axis, projected on the plane of the orbit, and the major diameter of the orbit, until in time the north pole will be headed directly away from the sun in that part of the orbit which the earth now occupies in September, and so on.

This diagram shows the successive positions of the earth at the Vernal Equinox (March 21st) due to the revolution of
the axis and the consequent westward movement of the First Point of Aries.
Fig. 1.
In the year A.D. 1250 the winter solstice occurred at perihelion and in the year 6400 A.D. the vernal equinox will occur at this point of the orbit. That is, the axis of the earth was inclined directly away from the sun at perihelion [Pg 30] in the former year but in the latter year the inclination will have changed about 90° backward against the earth’s course about the sun, and it will be the beginning of spring (the vernal equinox) when the earth is at perihelion instead of the first of winter as in 1250 A.D. Since 1250 A.D. the inclination has changed an equivalent of about 11 days for now the earth is at perihelion about January 1st, and the solstice occurring about December 21st, shows the present relative situation.
In other words, the vernal equinox is slipping back in the orbit towards the perihelion, and as the solstices maintain their positions at 90° from the equinoxes they must likewise be “slipping a cog” each year.
The vernal equinox was situated many centuries ago in the first part of the constellation of Aries, and was known as the First Point of Aries, but owing to the movement of precession it has dropped back or westward (as we face our southern horizon) 50´´ a year until it has left that constellation entirely and is now about leaving the constellation of Pisces, some 30° from the position used by Hipparchus in his calculations. The majority of navigators still call this point of the celestial vernal equinox the First Point of Aries.
Holding these facts in mind, it may be clear that as the earth approaches that part of the orbit where the vernal equinox occurs it has turned its pole, and correspondingly points on the equator, 50´´ to the right or west during the year; thus causing the point of the terrestrial equinox to meet (or come under) the sun that much sooner. In other words, referring to the effect as seen on the heavens, the celestial equinox was advanced [Pg 31] to the westward that much to meet the sun in its eastward movement among the stars and will become the nearest point to the sun, 50´´ before the position of the equinox of last year. As the points in the orbit where the vernal equinox occurs year by year works back toward the perihelion, the range line through the sun to the heavens beyond must each year correspondingly edge its way westward along the celestial ecliptic through different constellations. This is what is known as the precession of the equinoxes.
The course of the celestial pole in the heavens is shown by a circle drawn about the pole of the ecliptic using 23° 28´ as a radius. This path will pass 1¼° from our pole star and this position marks the present termination of our extended axis; half way around the circle it passes the first magnitude star Vega close aboard, thus making this the future pole star some 12,000 years hence. If there be such creatures as navigators in those far-away days, latitude by Vega will no doubt be a popular sight among them.
The cause of this remarkable movement of the earth is due to the fact that the earth is not a true sphere, and the influence of the sun is not exerted equally upon its mass. Its flattening at the poles is attended by a corresponding bulging along the equatorial belt. When the earth is in the vicinity of the perihelion, leaning away from the sun, the half of this ring of extra matter on the side towards the sun is above the plane of the ecliptic or orbit. The tendency of the added attraction exerted upon it, is to draw the earth to an upright position, or in other words, at this time the sun is pulling stronger on the [Pg 32] northern or upper side than on the lower. Again, when near the aphelion and summer solstice, leaning towards the sun, that part of the ring of extra matter on the side towards the sun is below the level of the orbit, and the attraction is again tending as before to pull the earth upright. At the equinoxes there is an equal amount of this extra matter above and below the plane of the orbit evenly distributing the attraction.
The effect of this influence would in time bring the earth’s equator and the plane of the ecliptic into coincidence and the earth’s pole would be directly beneath the pole of the ecliptic, were it not for its rotation. The two forces acting upon the earth result in the slow revolution of the axis. The exact effect of these forces is rather complex but it is a demonstration of the principle of the gyroscope. The movement of the axis is affected very slightly by other influences than that of the sun, the most notable of which is the moon, whose monthly revolutions around the earth produce a similar influence in the bulging mass within the tropics, but as its revolutions are so rapid, it has but a slight effect on the precession movement of the earth. It is sufficient, however, to cause the extended axis to nod slightly and make a waved circle of precession on the heavens. This is called “Nutation,” from the Latin word nuto, meaning to nod.
A thorough understanding of time, one of the most important elements in navigation, clears the way to a better idea of the theory of finding one’s position at sea; there is, in the minds of many, considerable fog hanging about certain portions of this subject, and it is hoped that this explanation will clear some of this away.
Worcester’s Dictionary defines time as measured duration. It is the interval between events. It flows ceaselessly and with uniformity, yet the mortal mind is unable to conceive its beginning or its end. Man, in order to measure his activities, has blocked it off into different denominations convenient for his uses. Of these, the navigator uses the following in his determinations and reckonings: years, months, days, hours, minutes and seconds.
Certain astronomical phenomena were naturally enlisted by the ancient astronomers to furnish standards for time measurements; the value of a year was determined by the time necessary for a complete revolution of the earth around the sun, while the length of a day was fixed by the time of a rotation of the earth on its axis. The precision with which these evolutions are accomplished gives the required accuracy. The revolution of the earth governs the change of seasons, while the rotation is responsible [Pg 34] for the alternating periods of day and night. With the exception of the month, the other measurements of time mentioned above are denominations of these standards. The month, one-twelfth of a year, is measured by the revolution of the moon around the earth.
Solar time, as its name implies, is measured by the apparent diurnal movement of the sun. It is the variety of time in universal use by which is regulated the daily activities of life; and this is indeed quite natural, for of necessity the work and play of the world depend upon the light and darkness that this body serves out to us.
While we are unconscious of the earth’s rotation, its effect is seen in the apparent daily course of the sun across the heavens, caused by our turning past it, yet in common practice the sun is assumed to revolve around the earth, and is usually thus spoken of for the purpose of simpler explanation.
The time at each meridian is necessarily different from that of every other, as only one of them holds the same position relative to the sun at the same time or putting it in another way, only one meridian can cross the sun at the same time, determining local noon for those places located upon it. It is forenoon for that part of the world westward of the sun and afternoon for that portion eastward of it. As the earth turns from west to east, the places or meridians to the eastward are first favored with the sun’s light, and those meridians cross this body before those to the westward. The sun apparently moves from the eastward to the westward, crossing each meridian in succession until in a few hours it is afternoon for places to the eastward and noon with us. The [Pg 35] sun is now in our meridian, and it is forenoon for people to the westward of us. For example, at 7 A.M., 75th meridian time, it is noon in England and dead of night in our Pacific Coast; at our noon (75th), it is late afternoon in England and breakfast time in California.
It requires 24 hours, solar time, for the sun to make its apparent revolution around the earth, this course being a circle; it contains 360° of arc. It follows that in one hour it passes over 15° of arc, while 4 minutes are required for 1° to be traveled. Thus it is evident that any arc of the circumference of the earth, or difference of longitude, which is the same thing, has an equivalent time value and vice versa. That is, the arc comprised between the meridian of Greenwich and the 60th meridian west, for instance, besides being measured as 60° W., is equal to 4 hours of time. Again 4 hours of Greenwich time indicates that the sun has crossed the Greenwich meridian 4 hours ago and is at that particular instant crossing the meridian 60° west of Greenwich. If the arc were between Greenwich and a place 60° E., the equivalent time interval would also be 4 hours, because 60° of arc is everywhere equal to 4 hours of time; but the time at Greenwich, with sun on the 60th meridian east, is 20 hours of the previous day, or 8 A.M. of the present day. Thus: May 14, 20 hours, or May 15, 8 A.M.
The meridians extend from pole to pole, and it matters not what parallel you may be on, whether north or south latitude, your distance can always be measured to the Greenwich meridian in arc or time precisely as well as though you were on the exact parallel of Greenwich itself. If the time at Greenwich is carried, and the local time of [Pg 36] any other meridian is desired, turn the difference of longitude into time and apply it with regard to signs: - if west of Greenwich and + if east. The local time at any place can thus be calculated; or to go farther, if the time of any meridian is at hand, the time of any other place can be readily found.
Every meridian carries a time of its own, and the instant of the click of a telegraph key may be recorded all over the world in the local time of each locality, yet the interval between this and a subsequent click has an absolute value which is the same at every place, regardless of whether it is expressed in solar, sidereal or lunar time, and its actual value is invariable.
For convenience, on land, our country is blocked off into belts of standard time, 15° wide, each carrying the time of its central meridian. For instance, 75th meridian time is used by the eastern states, while just westward the clocks’ faces show an hour earlier time, that of the 90° belt, and so on.
It is a good rule to remember in reckoning all kinds of time that the clock’s face shows earlier time to the westward, and from this it is easy to deduce the proper application of a correction.
There are two kinds of solar time used in navigation; the first to be considered is apparent time, the kind shown by the sun dial, or measured by the sun as we see it. It is noon of the apparent day when the sun is seen with the sextant to dip while taking a meridian altitude. It is at the moment of dipping that the navigator announces 12 o’clock, and with the striking of eight bells begins a new apparent day on shipboard.
[Pg 37] The Day Lost and the Day Gained.—The fact that the sun seems to travel from east to west, determining the local time for successive meridians or places along the way, causes an interesting condition in reckoning time aboard ship. A vessel steaming westward on a parallel sails with the sun; in the forenoon she is sailing away from it, at noon the sun overhauls the vessel and they race together, but it becomes a hopeless chase for the steamer during the afternoon. In consequence of their similar course, however, the vessel will hold the sun longer, and the length of daylight will be increased over that time allotted a stationary position in proportion to the speed of the vessel. On the other hand, a vessel steaming eastward each hour advances to meet the sun; at noon the effect is as if they pass each other, and during the remainder of the day they are moving in opposite directions, hence this vessel has a shorter term of light and is deprived of its full share of sunshine.
In practice these facts require the continuous setting back of the ship’s clock, keeping apparent time on a westbound vessel. Take a concrete case for illustration: to-day assume we are at sea on the 45th meridian west and set the clock at the dipping of the sun, apparent noon; the vessel is westbound, steaming along the equator, and rolls along at a good 15-knot clip. In 24 hours by the clock we will cover 360 miles, or 360´ of arc on the equator, which is equal to 6° difference of longitude. (Should the easting or westing be made in higher latitudes, the difference of longitude will be increased proportionately.) So when the ship’s clock shows noon we will be 6° farther west than at the preceding noon, or in 51° west. The [Pg 38] navigator, should he observe the sun, would find it had not reached its highest altitude (the meridian), and he would be obliged to wait (approximately) 24 minutes, the equivalent in time of 6°, before the sun would dip. The clock is carrying 45th meridian time, and we are now determining noon for the 51st meridian. He sings out 8 bells, but the clock shows 12.24 P.M. The ship has gained 24 minutes by sailing with the sun, and the clock is set back and a fresh start is made.
A vessel sailing east has the opposite experience. The navigator, if guided by the ship’s clock, would find that the sun had dipped some 24 minutes before noon if a run similar to the above mentioned was made eastward. In this case the apparent time of the 51st meridian is shown by the clock, while the ship has moved on to the 45th, and the time of noon is correspondingly approximately 24 minutes earlier than the clock admits.
In the above example, the clock in the first instance is 24 minutes fast and is set back that amount to correct it for the time of the 51° meridian W.; but this time cannot be thus arbitrarily thrown away without some subsequent reckoning. There is just so much time all over the world, and there are no gaps or extra intervals; it is absolute in its uniform flow. Therefore, there must be a way of squaring ourselves with Old Father Time.
But let us follow the voyage farther and see what transpires: Continuing the course westward and ignoring for convenience all intervening land, each day it becomes necessary to set the clock back 24 minutes until we have circumnavigated the earth. Suppose we took our departure from the Greenwich meridian and kept our log [Pg 39] throughout the voyage with great care, expecting, according to our reckoning, to arrive on a Saturday, we would indeed be mystified on arrival to hear the ringing of church bells and find that it was Sunday. We have lost a whole day according to our log, by throwing away 24 minutes at a time. The time of the world goes on just the same, regardless of how we juggle the hands of the clock. Now, if we try a similar voyage eastward around the earth, we will be setting the clock ahead 24 minutes each day, and when the anchor is dropped on our return, we will discover that it is Friday instead of Saturday. The ship’s clock has skipped this 24 minutes each day, and our log is a day ahead of what it should be.
In order to prevent this difference of date, it was decided years ago to establish an international date line, which should correspond approximately, with the 180th meridian. The logs of vessels going west around the earth will be a day behind the calendar when they reach Greenwich, so a day is dropped from the reckoning when crossing the 180th meridian; that is, if it is Monday, the next day in the log will be Wednesday. On the contrary vessels bound eastward will be a day ahead when they reach their destination of Greenwich, so the date of crossing the date line is entered twice in the log, as for instance, there will appear two Mondays. By this method the accumulated errors of chasing local time, are in a measure straightened out, and ship’s logs are kept in agreement with the calendar of those at home. Thus it will be seen that it is the accumulation of time thus gained or lost that obliges navigators to add or drop a day to or from their logs when crossing the 180th meridian.
[Pg 40] In slow cargo steamers and sailing vessels, particularly when the course creates but little departure, the change of time due to difference of longitude is not sufficiently large to cause much inconvenience and can be taken care of by setting the clock back or ahead at noon. But with the development of the modern steamer, speed has increased to such an extent that the easting or westing of certain day’s runs correspond to a considerable amount of time, and to correct the clock to local time, all at once, would be a source of inconvenience and a bother. This is especially true where a fast steamer covers much easting and westing in high latitudes where the convergence of the meridians has shortened the degrees of longitude, thereby increasing the difference of longitude over a similar day’s run in lower latitudes. Hence, in order to more equally distribute its error, the longitude at noon is anticipated by the navigator and the clocks set at 8 A.M. for the local time of the approaching noon meridian.
When the clocks are set at noon, they are correct only for the moment and then start an accumulating error, depending in amount upon the rapidity of the easting or westing made. But by anticipating the longitude at noon, the forenoon watch will experience a decreasing error instead of one accumulated for twenty hours, and still increasing. It serves to keep the time of day more nearly correct.
In the transatlantic service, where high speed is maintained and the courses result in a large amount of easting and westing, another method is used for convenience. The navigator estimates the noon position of the next [Pg 41] day and accordingly divides the error into thirds. The amount of the first third is applied at 11 P.M., the second at 3 A.M. and the last third at 5 A.M. By this method the error is distributed between the “first,” “mid” and “morning” watches. It is a matter of considerable moment, and no joke, to the hard-working stokers to have the clock set back on them the full amount of the day’s run all at one time; and likewise going east, it would be giving an unfair advantage to those on duty to set the clock ahead nearly an hour during the morning watch.
The apparent or real sun is not a very accurate timekeeper and its days are unequal in length. The aborigines and even our ancestors were content with the time of day indicated by the sun dial, but as the generations have passed, each bringing increased development, time has become valuable; the crude timepieces have been forced aside by more reliable instruments until to-day we figure down at times to a one hundredth part of a second.
It is impossible to construct a clock that will follow the irregularities of the apparent sun, so an imaginary sun has been devised which is assumed to make its revolution at a uniform speed along the celestial equator with exactly 24 hours between its transits of the same meridian. This interval is the average of all apparent days in one year.
The varying rate of the sun’s apparent motion is due to several causes which will be subsequently discussed under the Equation of Time.
The time measured by the transit and progress of the mean sun is called mean time; if at Greenwich, it is Greenwich mean noon and Greenwich mean time (G. M. T.); if it represents the time of the observer’s place or [Pg 42] meridian, it is local mean time (L. M. T.). It is mean time that is shown by all clocks and chronometers used in every day life.
The distance between the apparent and mean suns, expressed in time, is known as the Equation of Time, and the application of this correction depends upon which sun is ahead. It is tabulated in the nautical almanac for every two hours of Greenwich mean time, with hourly differences, so it can be reduced for longitude in time to any meridian, or corrected to any intermediate Greenwich time. It is applied according to the sign accompanying it, and can be used to change apparent into mean, or mean into apparent time.
The progress of the mean sun across the sky with reference to the meridian is measured by the angle at the pole (expressed in time), between the meridian and the hour circle passing through the mean sun. This is the hour angle of the mean sun as well as the local mean time.
Civil Time is a variety of mean time, and is reckoned through 12 hours from midnight to noon, and again 12 hours from noon to midnight, dividing the day into the well-known periods of A.M. and P.M. With this kind of time, the day begins at midnight and the hour angle until noon is measured eastward through 180° of the revolution and westward through the remaining half from noon to midnight. In other words, 4:00 P.M. signifies that the sun has a westerly hour angle of 4 hours, while 8:00 A.M. indicates that the sun is 4 hours eastward of the meridian.
Astronomical time is reckoned westward through the [Pg 43] whole 24 hours of the day, 0 hours being noon. From noon to noon is an astronomic day. Thus 5 P.M. civil is the same as 5 hours astronomical time, while 5 A.M., May 14th is the same as May 13th, 17 hours.
In every solar observation for time the real or apparent sun is observed and hence the time derived from the sight must be local apparent; to which the equation of time must be applied to convert it into local mean time. It has already been made clear that the longitude is equal to the difference between the local mean time and Greenwich mean time, or between local apparent time and Greenwich apparent time.
Sidereal Time
Sidereal is derived from the Latin word sidus, meaning of or belonging to the stars. Sidereal time is measured by the apparent diurnal revolution of the stars, resulting from the rotation of the earth. By their use the conditions which render the sun inaccurate as a timekeeper are eliminated; for the period of rotation of the earth is so regular that the passages of the stars across the meridian occur with great precision. This exactness enables the astronomer to keep the observatory clock checked to a remarkable degree of accuracy. These observatory clocks carry sidereal time, and for convenience it is customary to divide their faces into 24 instead of 12 hours.
Sidereal time is the bedrock of all time; for it is by converting it into solar time and sending it throughout the country by telegraph and radio that the people of [Pg 44] the world get the standard by which to set their clocks and chronometers. Sidereal time is not practicable for every day use as its noon occurs, without regard to light or darkness, at every hour of day or night during a year. In March, at the time of the vernal equinox, it agrees with the solar clocks, but in September at the autumnal equinox, its noon occurs at the solar midnight.
While the sun is employed as the object of reference in solar time, it may appear strange that no particular star is thus used in sidereal; but in lieu of a definite stellar object by which to measure the sidereal movement of the heavens, we refer to the celestial vernal equinox.
This point was located in the constellation of Aries centuries ago, and hence its popular name—The First Point of Aries; but this has become a misnomer, for the point has long ago moved westward into another constellation, as discussed under the Precession of the Equinoxes. Navigators still cling to the name, however, and the equinox continues to serve its purpose, regardless of its slow drift westward.
This imaginary point of reference crosses the observer’s meridian much as the stars do, with the difference that it is always on the celestial equator and acquires no declination. The value of this point becomes further enhanced by the fact that it always lies in the same direction regardless of our position in the orbit. In other words, the distance of the equinox being infinite, lines drawn from perihelion and aphelion, respectively, to it, fail to produce an appreciable angle.
In explanation of this statement, it must be understood that for all uses on the earth the terrestrial system [Pg 45] of direction (that is, using the bearing of the north pole as a standard, with east to the left and west to the right when the back is toward the pole) is entirely adequate, but when dealing with the direction of celestial bodies, a broader standard must be considered. North and South both have a definite place in the heavens, being the points of the extended axis of the earth, but east and west are only relative expressions. To demonstrate this: it is possible for a man, traveling westward on the Trans Siberian Railroad, to see from the rear platform, in the evening, a certain star bearing eastward. At the same moment it is possible for an officer of a transpacific liner in the early morning, to be taking a sight of this same star bearing westward. In terms of absolute direction that star bore the same from both sides of the world.
On the 21st of March the earth, sun, and celestial vernal equinox are in range, with the sun between the earth and the equinox. For a place in north latitude on the meridian of the terrestrial equinox, the sun as usual bears south at noon this day, and hence the range mentioned above bears south at that time.
This coincidence of bearing is only momentary, for the earth with its onward motion immediately moves out of range and forms an angle between the sun and the celestial equinox. At noon on the day succeeding the equinox the sun bears to the left of the so-called First Point of Aries (celestial vernal equinox). The sun according to terrestrial direction always bears south by true compass at noon, yet the First Point of Aries being at an infinite distance always bears the same by absolute direction. If this point could be seen and a bearing of it taken [Pg 46] by compass simultaneously with the sun, it would be, perhaps, S. 1° W. and so on widening the angle, roughly speaking, a degree each day.
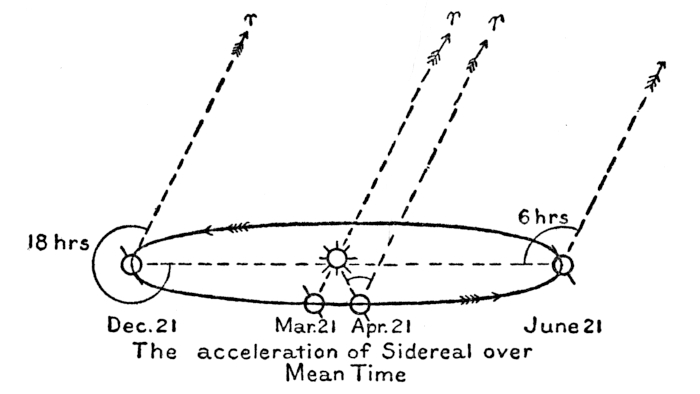
The acceleration of Sidereal over
Mean Time
Fig. 2.
The interval between two successive transits of the sun across the meridian constitutes a solar day, and likewise the period required for a certain star to return to the same meridian is a sidereal day, but these two days are not of the same length. The solar day we know is 24 hours long, but its sidereal contemporary has a length of only 23 hours, 56 minutes (approximately) solar time. The sidereal clocks, however, are geared to show 24 hours, sidereal time, in 23 hours, 56 minutes, solar time. By this it will be seen that in any given period the face of the sidereal clock will show more hours than the solar clock.
Both the solar and sidereal clocks start even at the vernal equinox, about March 21st, but from then on, the [Pg 47] sidereal clock gains on the solar time clock about 4 minutes a day until in a year it is a full 24 hours ahead, showing that there is one more day in a sidereal year than in a solar year. The approximate relation of the times shown by these clocks is readily calculated by allowing a gain in the sidereal clock of one hour for each 15 days after March 21st, or two hours for each month.
In order to aid in a simpler explanation, let us again follow the earth around its orbit and note the conditions that distinguish sidereal from solar time. Let us once more assume it to be the time of the vernal equinox, the clocks, both sidereal and solar, now show 0 hours, and the sun, the earth and the First Point of Aries are in range. The earth immediately moves out of line by virtue of its onward motion, and the sun correspondingly appears to move eastward; this is imperceptible at first, however, and not noticeable without a careful measurement, as it seems to be swallowed up in the contrary (westward) diurnal movement.
After 24 hours of rotation from the instant of the equinox the earth turns the meridian until it causes the First Point of Aries to transit, marking sidereal noon of the first day. The sidereal clock at this moment reads 24 hours, but a glance at the solar clock shows 11 hours 56 minutes A.M., about 4 minutes short of (solar) noon. An observation will show that the sun has apparently moved about a degree eastward of the hour circle passing through the First Point of Aries since the preceding noon, and the earth must turn this extra degree before the sun will be brought to the meridian, thus occupying the 4 minutes mentioned above. In other words, the earth turns [Pg 48] 360° in a sidereal day but must turn about 361° in a solar day.
Three months after the vernal equinox, the angle between the First Point of Aries and the sun becomes, in round numbers, 90°, and it requires 6 hours for the earth to bring the sun to the meridian after the passage of the First Point of Aries. In plainer language, when the First Point of Aries crosses the meridian (sidereal noon) the sun is about 90° to the left—about rising in the eastern sky; the earth must make a quarter turn, or 6 hours, before it will be solar noon. Thus it will be seen that at this point sidereal time is 6 hours ahead of solar time.
In six months, when the First Point of Aries is on the meridian the noonday sun is shining on the antipodes, and it lacks 12 hours of solar noon. The difference between the sidereal and solar clocks has now reached 12 hours and through a continuation of the same process the interval between their readings, widens throughout the remainder of the year.
When the 21st of March comes around again, and the meridian presents itself to the sun and the First Point of Aries in range, a careful count of the number of times this latter point has crossed the meridian during the year, discloses 366¼ transits. That is, the earth has actually turned about its axis 366¼ times. The sun is found to have passed the meridian only 365¼ times. Counting the rotations of the earth by the number of the sun’s transits while we are revolving around him, causes the apparent loss of a day due to the earth unwinding itself once, so to speak, during the year. The accumulated difference amounts to one sidereal day. Hence it will [Pg 49] be seen that a year contains 366¼ sidereal days of 23 hours, 56 minutes each, and 365¼ solar days of 24 hours each.
Now for a recapitulation of the subject of time.
The rotation of the earth is the real standard of measuring time intervals; the period required for this rotation does not vary. It has been suggested that the tide waves have a minute effect on the regularity of this movement, but the construction of our clocks is such, that if any variation exists we are unable to detect it. Whether we use the passages of the stars, or the transits of the sun to reckon our time, it falls back in either case upon the diurnal rotation of the earth.
Apparent time is measured by the seeming progress of the actual sun. The time of its transit of the meridian is irregular, but is always shown by its “dip,” culmination, with the sextant.
Mean time is reckoned by the revolutions of a fictitious sun, called the mean sun, and the length of one of these revolutions is the average of a year of apparent days. This, owing to its uniformity, is the time used for the everyday purposes of life. The difference between apparent and mean time is called the equation of time, and, by applying it according to signs given in the Nautical Almanac, one can be converted to the other as desired.
Sidereal time is indicated by the position of the First Point of Aries relative to the meridian; it is star time. The stars make a complete revolution of the heavens in 4 minutes less time than is required by the mean sun. Therefore the sidereal day is that amount shorter than the solar day.
[Pg 50] The point of the celestial vernal equinox or First Point of Aries is a sort of celestial “bench mark;” besides indicating sidereal time, it serves as a point from which right ascension is measured eastward. This subject has been discussed previously, but as it is intimately associated with sidereal time, perhaps it may be made clearer since the latter has been so fully explained.
Right ascension is measured on the celestial equator, precisely the same as longitude on the earth, excepting that it is always measured eastward through the full 24 sidereal hours, contrary to the diurnal movement of heavenly bodies. Moreover, the meridian passing through the vernal equinox is called the celestial prime meridian, and sometimes the Greenwich of the heavens. There is another point of distinction, however, between this prime meridian of the sky and our meridian of Greenwich, which, while it does not effect practical navigation, has to receive consideration in the long run; our longitude values on the earth remain at all times constant, but owing to the precession of the equinoxes the celestial prime meridian is slowly moving westward, thus causing the right ascensions measured from it to become very slowly in error (50´´ yearly).
The hour angle of a body is the angle formed at the pole between the meridian and the hour circle passing through the body measured westward.
With all these important facts well in mind we will go ahead under a slow bell, through a few more statements which may be found a little perplexing. However, a careful study of the Time Diagram will, no doubt, drive away the haziness so often surrounding the subject of time.
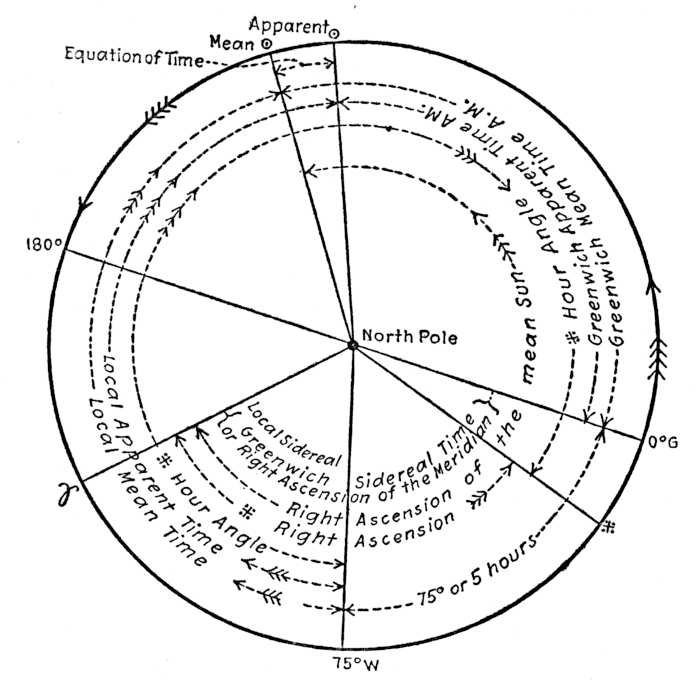
This diagram represents the plane of the equator looking down upon the
North Pole. The 75° W meridian is chosen as that of the observer and local time
reckoned therefrom. The arrows on the outer circumference indicate the directions
of the earth’s rotation; the other smaller arrows indicate the direction in which
each element is reckoned.
Fig. 3.
[Pg 51] The hour angle of the mean sun is the local mean time, and the hour angle of the First Point of Aries is the local sidereal time. The local mean time and longitude in time accelerated by Table III Nautical Almanac plus right ascension of the mean sun is equal to the local [Pg 52] sidereal time. The right ascension of the meridian is the same thing, exactly, as the hour angle of the First Point of Aries, and both of these are identical with the local sidereal time. The sidereal time of Greenwich mean noon is the same as the right ascension of the mean sun at that time. The hour angle of a star plus the right ascension of the same star is equal to the local sidereal time.
Difference of longitude can be represented by an interval of sidereal time or by a difference of right ascension, precisely the same as by a difference of solar time. Thus with the local sidereal time calculated from an observation of a star, and the corresponding Greenwich sidereal time taken from the Nautical Almanac, the longitude is at hand, by turning their difference into arc. The fact that the actual time interval is longer in the case of solar time than in an interval of the same number of hours of sidereal time, has no influence on the resulting difference of longitude. The number of degrees in any arc can be the same, yet vary in linear measurement, but the same number of hours of solar and sidereal time represent the same proportionate part of a circle. It was just stated that the hour angle of a star plus its right ascension is the same as the local sidereal time; now this is also true of the sun. The hour angle of the mean sun plus the right ascension of the mean sun is equal to the local sidereal time; by means of this equality we are able to find the Greenwich sidereal time on any occasion. It is necessary to have this element in order to compare it with the local sidereal time, which we find by observation of a star, to obtain difference of longitude (in time). In page 2 of the Nautical Almanac will be found the Right [Pg 53] Ascension of the Mean Sun at Greenwich Mean Noon; this must always be taken out for the preceding noon. We now have a measure of sidereal time to be added to a measure of mean time, but it will be remembered in early arithmetic that an apple and a peach can not be added together any more than ½ can be added to ⅓. The only course to steer is to reduce the quantities to a common denominator, or like quantities. So in handling these two varieties of time, solar time must be accelerated by adding a correction to it, or sidereal time retarded by subtracting an amount necessary to make it equal to a corresponding value of solar time. The tables for the conversion of one of these varieties of time to the other are found in the American Ephemeris Tables II and III, Bowditch Tables 8 and 9, and at the foot of pages 2 and 3, Nautical Almanac.
A practical illustration of this may make a clearer impression. In the early evening of April 8th, secured a sight of Regulus; the chronometer showed 8 days, 9 hours, 56 minutes, and 0 seconds (corrected), with other necessary elements given, the sight is worked as usual to find the star’s hour angle, which proves to be:
| h. | m. | s. | |||||
| H A Regulus | 1 | 59 | 47 | bearing west. | |||
| R A | 10 | 3 | 02 | RAMS | 1 h. | 6 m. | 7 s. |
| — | — | — | GMT | 9 h. | 56 m. | 0 s. | |
| L. S. T. | 12 | 02 | 49 | Accel. 9 h. | 1 m. | 29 s. | |
| G. S. T. | 11 | 03 | 45 | Accel. 56 m. | 9 s. | ||
| — | — | — | —— | —— | —— | ||
| Long. in time | 59 | 04 | G. S. T. | 11 h. | 3 m. | 45 s. | |
[Pg 54] This being a star sight we obtain from it the sidereal time at place of observation and as the chronometer carries Greenwich mean time we seek the corresponding sidereal time by adding this and its acceleration for a sidereal interval to the right ascension of the mean sun taken from Nautical Almanac. The result is the Greenwich Sidereal Time.
It is occasionally required to find the sidereal time at the ship in which case it is only necessary to apply the longitude in time to the Greenwich Sidereal Time.
As Greenwich mean time is the most used and is the best understood it is a very convenient practice to carry G. M. T. on the navigator’s watch. It is readily converted into any other time with ease but serves more purposes as it is without conversion. A stop watch is an excellent instrument for taking time sights where great accuracy is essential. By setting it at 0 minutes a man can observe alone starting the watch as he makes contact with the horizon and when subsequently comparing with the chronometer subtract the reading of the watch to get the G. T. of observation.
The most expeditious way to convert time into arc is to multiply the hours by 15 and add the number of minutes divided by 4 to get the degrees; multiply the remaining minutes by 15 and add the seconds divided by 4 to get the minutes; multiply the remaining seconds by 15 to get the seconds in arc:
Thus:
| Long. in time | 2 hrs. | 42 m. | 23 s. |
| 30 | 30 | 45 | |
| 10 | 5 | ||
| Long. in arc | 40° | 35´ | 45´´ |
[Pg 55] To change arc into time divide the degrees by 15 to get the hours; multiply the remainder by 4 and divide the minutes by 15 and add to get the number of minutes (m.); multiply the remainder of minutes (´) by 4 and divide the seconds (´´) by 15 carrying the division of tenths if desired, adding the result to get the seconds (s.):
Thus:
| Long. in arc | 40° | 35´ | 45´´ |
| 2 hrs. | 40 m. | 20 s. | |
| 2 | 3 | ||
| Long. in time | 2 hrs. | 42 m. | 23 s. |
This may appear complicated at first but is much the quickest way of conversion. However, Table No. 7, Bowditch is always available if desired.
In getting an understanding of any time problem, that is such as changing mean time into sidereal time; obtaining the hour angle of a star or planet; in seeking the local time from the chronometer, or any time values that are found perplexing, always draw a diagram. Make the circle on the plane of the equator, with the pole as the center, and meridians radiating from it towards the circumference of the circle. Now imagine for the moment that you are at the north pole, and the date is the 21st of September. The sun is traveling in the horizon, and if the direction of the Greenwich meridian is known, this body serves as a time piece, for the angle between this meridian (direction) and the sun is the Greenwich time. This angle corresponds with twice the angle between XII hours on the watch and the hour hand; or would (disregarding equation of [Pg 56] time) coincide with it if the watch’s face was divided into 24 hours. Likewise when the vernal equinox or First Point of Aries lies in the direction of Greenwich it is Greenwich sidereal noon, and the subsequent angle that appears through the rotation of the earth, shows the Greenwich sidereal time.
Equation of Time
It is necessary in considering this subject to reiterate some of the statements made in the preceding talk on time, but, as they are very important, no time is wasted by further impressing them on the mind. Let it be understood that the apparent orbit of the sun is actually due to the earth’s revolution around him, yet for simpler explanation it is considered to be the sun’s own revolution.
The apparent movement of the real sun is not of uniform speed and, in consequence, it has become necessary to devise a fictitious sun whose assumed revolutions around the earth are at all times regular in their rate.
The equation of time is the difference between these two suns and, as they are at times in conjunction and at other times attain a distance from each other of 16 minutes 20 seconds, and, moreover, as the real sun is sometimes ahead and again in the wake of the mean sun, it becomes evident that the equation of time is an ever varying quantity.
The irregularity of the sun’s apparent movement as compared with the uniformity of the mean sun, is subject to two causes: First, the earth travels in an ellipse, and, as the length of a degree varies in the different parts of the circumference, the motion would appear to be irregular, [Pg 57] that is, if the sun actually traveled at a uniform rate, it would, from the above fact, appear to us to be variable in its motion; furthermore, the laws of forces only allow a body traveling in a circle the privilege of a uniform speed so the earth, owing to its varying distance from the sun, experiences a corresponding change in the amount of attraction exerted upon it by the sun and its velocity, actually becomes variable. Thus, during the winter, December and January, when they are nearest each other, the attraction is strongest and the earth increases its speed in revolution; while in June and July the earth is at its greatest distance from the sun and the attraction is less, resulting in a slowing down in the rate of the onward movement. As the sun appears to us to take on movements corresponding to those of the earth, these variable movements of the latter are seen in the apparent motion of the sun. Second, the plane of the earth’s orbit is inclined at an angle to that of the equator, which makes the sun appear to be traveling at a variable speed along the ecliptic.
With these two errors combined influencing the apparent sun, he becomes unreliable for regulating timepieces. The mean sun, which was originated to obviate these irregularities, is assumed to travel in a circle with the earth located in the centre, which disposes of the first reason for an apparent variable motion; and again, the mean sun revolves in the plane of the equator, thus eliminating the second obstacle in the way of uniform time.
Now we will continue a little farther into the explanation of the reasons for the irregular movement of the real sun. A law discovered by Kepler, and named for him, provides that a radius from the sun to the earth covers sectors [Pg 58] of equal areas in equal times; a sector equal in area to any sector covered in the same time. That is, when the earth is in that part of the orbit near the vernal equinox, the radius of the orbit will in a given time, say a week, sweep over a certain area; the earth proceeds toward aphelion and when in the vicinity of that point, the radius becomes greatly increased in length. Now in a week with this longer radius, a far greater area would be covered if the earth maintained the same rate of speed as at the equinox, but Kepler’s law says, “equal areas in equal times,” so in order to conform with the law, the earth’s speed of revolution must be reduced. The earth does not slow down just for the sake of obeying Kepler, but at this part of the orbit it is at its greatest distance from the sun and hence the reduced attraction causes the earth to lag a little.
At the time of the autumnal equinox, an area similar to that of the vernal equinox is covered. As the earth approaches perihelion, the radius is gradually shortened by the eccentricity of the sun in this part of the orbit and the increased attraction causes the earth to speed up correspondingly. At the increased speed, the shorter radius sweeps the same area in a week as at other parts of the orbit and Kepler’s law still holds good.
As the apparent motion of the real sun corresponds exactly with the real motion of the earth, it is evident from the above that the real sun apparently moves at different rates of speed along the ecliptic, faster in winter and slower in summer than the mean sun.
The value of a mean solar day is the average of a year of apparent days, or in other words, there is the same number of mean solar days in a year as there are apparent days.
[Pg 59] In considering the effect of the variable motion of the earth in its orbit, we will recall the conditions used when defining sidereal and solar days. The former comprises the interval between two successive passages of a certain star across the meridian, or perhaps better, between two successive passages of the meridian over a star. This is the true length of the earth’s rotation and is the standard to which we may refer the length of the mean or apparent solar days.
Now it requires about 3 minutes 56 seconds longer for the meridian to sweep around from sun to sun than from star to star, owing to the fact that the mean sun moves uniformly eastward that amount daily, thereby requiring the meridian, after reaching its position of yesterday noon, to overhaul the mean sun this 3 minutes 56 seconds of eastward movement. The mean sun maintains this uniform difference between its days and the length of the sidereal day. Without this daily easting of the sun, the sidereal and solar day would be the same.
But, in considering the apparent sun, we find the length of its days continually varies from both that of the sidereal and mean day. This is explained by the fact that the eastward movement of the apparent sun is due to the movement of the earth in its orbit, and as this movement becomes faster or slower the eastward movement of the sun becomes correspondingly faster or slower. Thus, we readily see that with the apparent sun moving eastward faster or slower at times, the length of the apparent day must vary accordingly and we cannot establish a uniform difference between it and the sidereal day, as in the case of the latter and the mean day. The apparent days exceed the mean days in [Pg 60] length, between September and March, while the earth is traveling fastest in its orbit. Beginning at the autumnal equinox with the apparent sun eight minutes behind the mean sun, the former gains slowly at first but with increasing rapidity. About the end of December, at perihelion, it overhauls the mean sun and they are coincident as regards this correction only. Leaving perihelion, the apparent sun rapidly takes the lead but with a gradually decreasing amount until at the equinox in March, reaches its maximum lead of 8 minutes. Entering that portion of the year March to September, we find the earth traveling slower and the mean sun gaining on the apparent sun; between the vernal equinox and aphelion, the mean sun gains until both are together at the summer solstice and then forging ahead the mean sun attains a lead of 8 minutes in September.
It must be borne in mind that this error is caused only by the eccentricity of the orbit and is but a component part of the whole correction of the equation of time. The other portion is due to the obliquity of the orbit, or its inclination to the equator.
This error is introduced through the fact that the apparent sun moves in the ecliptic and the mean sun is assumed to proceed along the celestial equator. In considering this phase of the question, we will ignore entirely, for the time being, the error of eccentricity described above.
The error of equation of time due to the obliquity of the orbit is a simple one to see, but like many simple things it is easier to show it by a diagram than to explain in words, so the reader is referred to the accompanying figure, that a study of it may be made before proceeding.
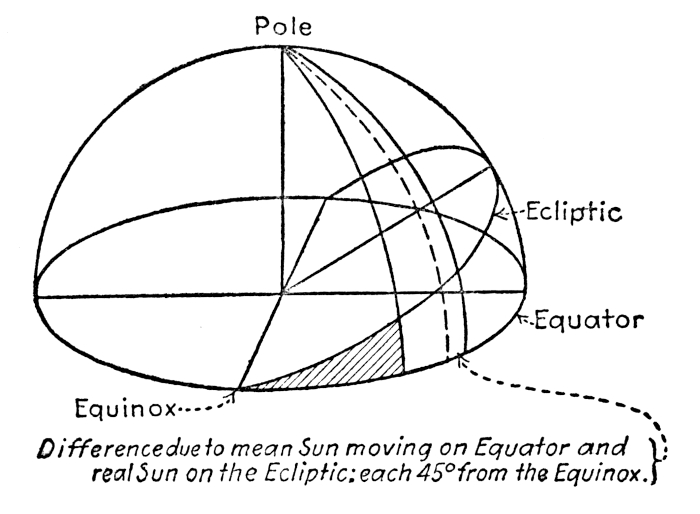
Fig. 4.
[Pg 61] At the equinoxes, where the ecliptic and equator cross and the solstices—the vertices of the ecliptic—that is, four times a year, the true and mean sun are together, but departing from these points they do not travel with the same right ascension, remembering that right ascension is measured on the equator. Taking, for example, the earth in that quadrant of the orbit comprised between the vernal equinox and summer solstice, the apparent sun in the heavens would be by cause of obliquity alone, to the right or to the westward of the mean sun, and thus it will be seen that with the earth rotating from right to left the apparent sun will cross the meridian first; consequently between March 21st and June 21st that part of the equation of time due to the obliquity of the orbit bears a minus sign when mean time is desired from the apparent time. This correction reaches its maximum half-way or 45° from the equinox, amounting at that point to nearly 10 minutes.
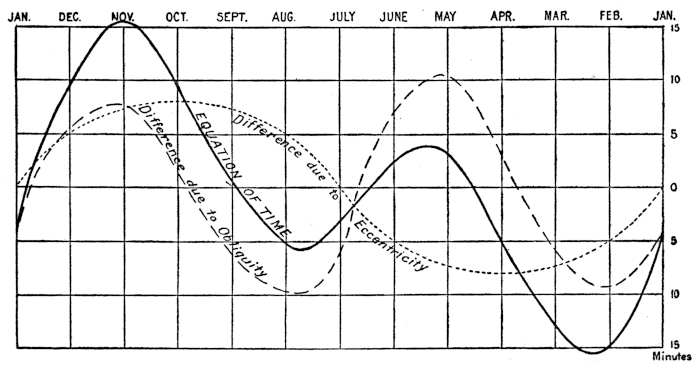
Fig. 5.
[Pg 63] Now the reason for this difference between the mean and apparent sun when each (so far as this problem is concerned) moves along its respective path—the equator and the ecliptic—at the same rate, is this: suppose the equator between the equinox and the solstice is divided into an equal number of parts and an hour circle drawn through each point of division. Beginning from the equinox (the common apex of the triangle) the arc of each hour circle between the equator and the ecliptic, forms the altitude of a right-angled triangle, while the equator and the ecliptic are base and hypothenuse respectively. Thus it will be seen that each portion of the equator (base) is shorter than the corresponding part of the ecliptic as defined the hour circle, to the extent of the ratio of the base to the hypothenuse.
This amount increases with the increasing size of the triangle, but a new element enters to counteract its effect. With the increasing divergence of the ecliptic and equator, the divergence of the hour circles becomes a factor and as the solstice is approached the divisions on the equator, are represented on the ecliptic by gradually decreasing spaces between the hour circles.
The combination of these effects produces the error due to the obliquity of the orbit. The error has the opposite effect in the next quadrant, that is, from June to September; and in opposite quadrants it is the same.
So it will be seen that error due to the eccentricity causes the apparent sun to lead the mean sun from December 31st to June 30th, reaching a maximum of 8 minutes about April 2d. This sun then falls astern until December, again attaining a maximum of -8 minutes about October [Pg 64] 1st. The error due to the obliquity of the orbit accumulates between the equinoxes and solstices for at these points the two suns are together and there is no error, but about the 6th of May, August, November, and February, it reaches a maximum of 10 minutes; in August and February, the mean sun takes the lead.
These two errors of equation of time combined algebraically will result in the plain line of the diagram.
Calendar
The ancients, in order to keep track of past events and to anticipate the future, devised a calendar, which, while not identical with the one now in use, was of itself a remarkable production. They chose the revolutions of the moon as their basis of measuring the passage of time, and, as a lunar month contains only 27⅓ days, the 12 months used in this early calendar comprised a year of about 354 days.
It became apparent as the world progressed that use of the moon was very unsatisfactory for this purpose, as the calendar became complicated and confusion resulted, owing to the difference between the lunar and solar years. This condition remained until the reign of Caesar, when that monarch determined to establish a more satisfactory method of reckoning time. With the aid of an eminent astronomer, he completely revised the calendar, using the revolution of the earth around the sun as the standard for the length of a year. The time required for this is 365¼ days, approximately, and as it was inconvenient to include [Pg 65] the ¼ day in the year, it was allowed to accumulate for 4 years, when as a whole day, it was added to the end of February.
Caesar, evidently proud of this accomplishment, honored himself by naming his astronomer’s invention the Julian Calendar and in order to further immortalize himself he changed the name of the seventh month to July. Augustus, his successor, apparently envious of the honor his predecessor derived from this source, and determined not to be thus outdone in perpetuating his name, changed the month Sextilis to August.
The commonly accepted 365¼ days as the length of year is only an approximation, however, and the small difference between this and the actual length of a year began to accumulate until this weak point in the Julian Calendar became a matter of moment. The exact length of a year from vernal equinox to vernal equinox is 365 days 5 hours 48 minutes and 46 seconds, which lacks just 11 minutes 14 seconds of 365¼ days. This caused the dates of the equinoxes and solstices to keep slipping back 11 minutes each year and when considerable time had passed the difference became large enough to cause inconvenience; the date of the vernal equinox having dropped back to March 11th in 1582. In this year Pope Gregory, acting under the advice of an astronomer by the name of Clavius, modified the Julian Calendar. He first added 10 days to restore the date, and then to forestall a further retrogressing of the calendar, provided that only those century years divisible by 400 should be considered leap years. In this way the 11 minutes 14 seconds was prevented from causing further mischief. This calendar known as the Gregorian Calendar [Pg 66] is now in almost universal use, though at first it was adopted only by Catholic countries.
It is interesting to note that the time consumed by the sun in making his apparent yearly revolution from a certain star back to that star again is a sidereal year of 365 days 6 hours 9 minutes 9 seconds. The tropical year—the one in common use—is shorter, being the time required for the sun to leave and return to the vernal equinox, or First Point of Aries. This point, it will be remembered, is moving westward about 50´´ annually, and it will be seen that while the sun starts its eastward revolution among the stars, the equinox is very slowly moving westward to meet him, thus making the tropical year about 20 minutes shorter than the sidereal year.
While discussing the calendar it is an opportune time to explain a matter concerning the dates of the equinoxes and solstices. It has of course been noticed by everyone that the vernal equinox occurs one year on March 20th and another on March 21st, or the summer solstice on June 22d and yet another year on June 21st and so on.
Aside from the slight change due to the dropping back of the seasons in the orbit by the precession of the equinoxes, the actual time of the equinoxes and solstices may be considered as constant, yet the dates vary a few hours.
The year in common use—the tropical year—contains approximately 365¼ days, yet we take account of only 365 days, the extra ¼ day being laid aside for future reckoning. During the next year this 6 hours will be augmented by 6 more; the next by another 6, making 18 hours ahead of the calendar. The fourth year this amount reaches 24 hours, and a full day, the 29th of February, is added to the calendar [Pg 67] for that year, and we are square again. But the different equinoxes and solstices occur at just 364¼ days; taking for example the vernal equinox, it occurs on the following (approximate) dates, which it will be noticed are 6 hours later each year:
It is evident by the above that the insertion of the extra day just previous to the equinox in the leap years, sets the date of the equinox back a day by the calendar. Juggling the ¼ day as shown above causes the change in the calendar dates of these phenomena.
The observed altitude of a heavenly body, as measured with the sextant, requires treatment for numerous errors to reduce it to the true altitude and make it ready for use in working any of the navigational observations. The amount of error varies in different bodies, the moon requiring the maximum and the fixed star the minimum correction. All the errors are not common to all bodies, that is, with some, certain errors become so insignificant that they are cast aside.
These errors comprise the index error of the sextant, refraction, dip, semi-diameter, and parallax. In Table 46, Bowditch, will be found the combined corrections (index error excepted) to be applied to an observed altitude of a star or planet and to that of the sun’s lower limb. A supplementary table furnishes an additional correction to be applied to the semi-diameter of the sun when accuracy is desired. These corrections will now be discussed in the order named:
Index Correction
The index and horizon glasses of a sextant are supposed to be parallel when the zero of the vernier and the zero of the limb are in one, and with this the case, the true and [Pg 69] reflected images seen in the horizon glass should exactly coincide. Any difference between them is the index error.
It is seldom that a sextant is so well adjusted that no index error exists, but it is not desirable to keep tampering with the instrument with an attempt to eliminate this error, for it will in time injure its accuracy.
By testing the sextant at each sight, the error can be closely watched and allowance made for it in correcting altitude. The easiest and most accurate method of ascertaining this error is by using a star in the following manner: Set the zero of the vernier a little to either side of the zero of the limb, and observe a 2d or 3d magnitude star—move the reflected image past the real and note if they pass directly over one another. If not, the horizon glass is not perpendicular and needs adjustment. Bring the reflected star in exact conjunction with the real star, and read off the index correction—if the zero of the vernier is to the left of the zero of the limb—on the arc—the difference is minus (-) and subtracted from the observed altitude; and if to the right—off the arc—it is plus (+) and added. A well-known rule of thumb expresses it thus: if it’s on it’s off, and if it’s off it’s on. The sea horizon is also available for determining this correction and serves the purpose with fairly accurate results.
Semi-diameter
In measuring the altitude of certain bodies for navigational purposes, it is necessary to determine the distance of the center of the body above the horizon. To accomplish this in an accurate manner the lower edge or limb is brought [Pg 70] down to the horizon and the semi-diameter applied to this measured altitude. When the lower limb is used, as is the usual practice, the correction for semi-diameter is obviously plus (+). The upper limb can be resorted to, however, should the lower side of the body become veiled by cloud, and in this case the correction is minus (-).
Semi-diameter of the sun is obtained readily from the Nautical Almanac for each ten-day period, for it must be remembered that the sun is continually changing its distance from the earth, and consequently the diameter of the former is increased and lessened slightly at different times of the year. For instance: On January 2d, when the earth is near perihelion and we are at our nearest point to the sun, the semi-diameter is 16´ 17´´.90, while on July 2d, when we are in the remote parts of the orbit, the semi-diameter is only 15´ 45´´.69, making a difference of over 32´´.
The moon being such a near neighbor of ours gives more trouble in determining her diameter. Besides being greatly affected by her rapidly changing distance from the earth, a further correction is occasioned by the fact that our position on the surface is nearer the moon at times than is the center of the earth. That is, when the moon is in the zenith we are 4000 miles, the earth’s radius, nearer that body than when she is in our horizon. It is evident that the direction of the moon in our sensible horizon is at right angles to a perpendicular erected at our place of observation and passing through the earth’s center, and this again makes it evident that the moon is about equally distant from the earth’s center and our position on the surface; but as she ascends the heavens she comes nearer our position [Pg 71] until in the zenith the distance has been reduced by 4000 miles and the diameter appears correspondingly larger. Draw a diagram and see for yourself. This Augmentation of the Semi-diameter, due to the altitude, is found tabulated in Bowditch, Table 18.
The semi-diameter becomes too small to consider in ordinary navigation when observing any of the planets, and of course fixed stars are beyond its scope.
Refraction
Everyone knows that the blade of an oar when dipped in the water appears to be bent in a remarkable manner at the surface. This is a clear case of refraction. Should the oar, however, be held under everywhere at an equal depth, a square look downward at it would fail to show any refraction. So it becomes evident that refraction is caused by the rays of light passing obliquely from a rarer to a denser medium or vice versa. A ray of light coming from a heavenly body to the earth passes through a medium of gradually increasing density, from the thin outer air to the denser atmosphere at the surface of the earth. The ray of light consequently becomes curved downward and reaches the earth at a point nearer the heavenly body than would be the case if the light ray traveled in a straight line. The effect of this to the observer is that the body appears higher than it really is. The difference between the actual direction of the ray of light unaffected by the air, and our line of vision as we see the body, is the refraction.
The amount of refraction ordinarily affecting an observed altitude depends upon the distance of the body [Pg 72] above the horizon. At the zenith, the rays of light, entering our atmosphere perpendicularly, are not deflected and refraction is nil. But, on the other hand, when the body is near the horizon, the rays of light pass through the atmosphere at a sharp angle and are consequently subject to the greatest bending, thus giving us our maximum refraction. In fact, this element becomes so unreliable in low altitudes that it is not advisable to observe a body when less than 10° or 13° above the horizon. This in no way concerns bearings taken of bodies in the horizon for amplitude, as refraction affects the altitude and not the azimuth of a body.
Dip
It is a well-known fact to every seaman that by going aloft, he can pick up a light sooner than on deck; that is, the higher his elevation the wider his horizon becomes. The horizon of a man in a small boat is only about 3 miles away, but, if he climbs to the bridge of a steamer some 60 feet above the water, he finds that the horizon has receded until he has a range of about 9 miles.
The fact that the horizon can be altered by changing the altitude should appeal to every navigator as a possible means of getting a horizon in foggy weather, by going aloft or getting as low as possible, provided the fog bank is lying above or close to the water.
The altitude of a body is measured to the visible horizon, yet the measurement must be adjusted to the sensible horizon before the true altitude can be obtained. This correction is accomplished by applying to the observed altitude [Pg 73] the amount of the angle formed at the observers eye by the planes of the sensible and visible horizons. The angle is known as the dip of the horizon. It is readily seen that this angle always makes the observed altitude too large, for the eye if located at the exact surface of the sea, theoretically sees the sensible and visible horizons in one, while at every elevation above the surface it depresses the visible horizon correspondingly. It is, therefore, always necessary to apply the dip as found in Table 14, Bowditch, with a minus (-) sign.
An inspection of the table of dip will show that the rate of increase of this error becomes more rapid as the height of the eye is diminished. To illustrate: The reader will note that between an elevation of 4 feet and one of 9 feet there is a difference of 1 minute in the dip, while higher up, say between 26 feet and 38 feet, a difference of 1 minute is likewise found, yet in the first instance there was a range of 5 feet and in the second a range of 12 feet. This fact in itself is an argument in favor of observing altitudes at a good height above the water.
In calculating a meridian altitude, an error in the dip directly affects the result by a corresponding amount, so extra care should be exercised in this respect. In this instance, we endeavor to locate the body relative to our zenith and anything that affects its altitude directly affects the latitude. In a time sight, a different principle is involved. Here the position of the body as defined by the latitude locates the apex of one angle of the astronomical triangle and hence a small error in the altitude will very likely cause a greater effect on the longitude.
An allusion was made under the caption of Refraction [Pg 74] to the displacement of the visible horizon by terrestrial refraction to detect which requires watchfulness on the navigator’s part. The familiar “loom” seen along the coast is an example of the workings of variable refraction. Now imagine this distortion less aggravated with no land to show its existence and you have a good illustration of this error.
Refraction of this nature is usually found during light airs and calms when the different layers of air arrange themselves according to their temperatures. The heated air over land below the horizon in hot weather will displace the intervening horizon; moreover, when the air is warmer than the sea, the horizon is elevated above the normal and, when the conditions are reversed, the horizon is unduly depressed. Thus lights become visible a little sooner after a hot day ashore. The Red Sea, Gulf Stream, mouth of the Amazon, and other large rivers are places where the horizon should be especially distrusted. Capt. Lecky, in his famous Wrinkles in Practical Navigation, refers to an experience he once had with this error. The latitude had been found “by an excellent meridian altitude of the sun to be as much as 14´ in error. The time was mid-winter—the day a clear cloudless one—the sea smooth, and the horizon clean-cut. Five observers at noon agreed within the usual minute or half minute of arc, nevertheless, on making Long Island (U. S. A.) in less than two hours afterwards, the latitude was found wrong to the amount stated. Many such cases have come under the writer’s notice, but this one alone is cited on account of the magnitude of the phenomenon.”
What Captain Lecky said in his work on navigation is [Pg 75] reliable and this should serve to make an impression as to the dangers of such occurrences.
In clear weather this displacement of the horizon may be lessened somewhat by observing from aloft. By extending the horizon, such disturbing influences as the motion of the vessel and an irregular horizon caused by rough sea are minimized. In hazy weather, however, it is recommended to observe low, bringing the horizon as close as possible.
Parallax
In calculating the true altitude of a body the distance of its center above the horizon is supposed to be measured from the center of the earth, or what is the same thing, the altitude above the rational horizon.
The application of semi-diameter adjusts the measured angle with the center of the body, while parallax corrects the error due to our observing from the surface of the earth to the sensible horizon, instead of from the center to the rational horizon.
Parallax, in other words, is the angle formed at the body by the lines drawn from the observer’s position, and from the center of the earth, respectively. This angle is subtended by the radius of the earth, and it is obvious that the farther away a body is, the smaller the angle, and consequently the less the parallax. So when dealing with planets or fixed stars, it becomes insignificant and no parallax is considered.
The moon, on the contrary, is so close aboard that the angle of parallax reaches a value of nearly 1´; as a [Pg 76] minute of altitude means a minute of latitude and in turn a mile, so with this body the error due to parallax must be carefully determined.
In the case of the sun, however, it is somewhat of a waste of time to bother with parallax, for it never exceeds 8´´ or 9´´ and such fine calculation is uncalled for in ordinary navigation where so many greater errors must be kept in sight. However, we desire to eliminate every known element of error without undue figures, so it is recommended that Table 20B, Bowditch, be used, where without extra trouble the parallax may be found conveniently combined with the refraction.
When a body is in the sensible horizon, the parallax is greatest. The angle of parallax subtended by the radius of the earth is then an acute angle of a right-angled triangle and is as large as it can possibly be with the body at the same distance. As the body obtains altitude above the horizon, the right angle of the triangle (at the observer) becomes obtuse and our acute angle of parallax becomes smaller and smaller until the body reaches an altitude of 90°—in our zenith, when the obtuse-angled triangle has resolved itself into the perpendicular line that passes through our position and the earth’s center. The angle of parallax here disappears.
When a body is in the horizon, its parallax is known as Horizontal Parallax in contra-distinction to Parallax of Altitude. The latter has become generally known among navigators merely as parallax.
Our position on the surface causes a body to appear lower than if viewed from the center of the earth, so the error of parallax is added to the observed altitude; when, [Pg 77] however, it is combined with refraction it is subtracted in an observation of the sun, but added when the moon is used.
The parallax of the moon is excessive because the radius of the earth becomes a considerable amount when compared with the close proximity of the body, and causes a considerable angle at the body between the lines drawn from the observer and that drawn from the center of the earth. The change in parallax is so great that it becomes necessary in order to preserve accuracy to correct the observed altitude for index correction, dip and semi-diameter, to secure an approximate corrected altitude before attempting to correct for parallax. The horizontal parallax, which is the angle subtended by the earth’s radius when the moon is in the horizon, is taken from the Nautical Almanac, and with this and the approximate altitude as arguments, enter Table 18, Bowditch, and pick out, having regard for correction tables at the right, the parallax and refraction combined.
The usual corrections to the observed altitude of the sun or stars can be picked out at once from Table 46, Bowditch, where they are all combined for a quick correction.
Meridian Altitude
It is surprising to us, in these advanced days of nautical science, to read of our adventurous ancestors of a century ago navigating their ships to all parts of the known and unknown world with nothing to guide them but their dead reckoning and the latitude crudely obtained by the method of meridian altitude. Many of our finest ships, as late as the first decade of the nineteenth century, sailed to China and back with no knowledge of their longitude save what the master guessed it to be. Even in later days much navigating has been done in the less lucrative trades by mariners who had no knowledge of the method of finding longitude. It required more time and distance to navigate by latitude and dead reckoning only, as it was not always safe to lay a course from an indefinite position directly for the coast. It was the custom in the old days to keep off soundings until on the latitude of the port of destination, then steer due west, and whatever the longitude might turn out to have been the master would sooner or later make the land in the vicinity of his port.
The first step in obtaining the latitude by meridian altitude is the measurement with the sextant of the sun’s altitude. This is done when it reaches its highest point [Pg 79] in its course across the sky; this occurs when it bears due N. or S. true and this moment is local apparent noon. A few minutes before this time the image of the sun should be brought to the horizon, and by swinging the lower part of the instrument the image will be made to swing likewise in an arc; the lowest point of its lower edge (limb) should then be brought in contact with the horizon as closely as the circumstances will permit. The image will keep rising from the horizon, but by using the tangent screw it can be continually brought back to contact. At noon it will hang, and dip below; the reading of the sextant at this moment is the meridian altitude.
In working the problem three quantities are used and the navigator must be familiar with them:
The first is the zenith distance (z), which as its name implies is the sun’s (or stars) distance from the zenith. Zenith is 90° from the horizon, so the true altitude of the body subtracted from 90° is z the quantity desired.
The second element is the declination (d), which is the distance in degrees, minutes, seconds, of the body either north or south of the equator. This is taken from the Nautical Almanac.
The third and resulting quantity is the latitude, which is the distance in degrees, minutes, seconds, of the ship either north or south of the Equator.
The altitude observed taken with the sextant at noon is corrected for semi-diameter, parallax, dip, refraction and instrument error (if any exists). These corrections are explained in detail in Corrections for Observed Altitudes.
The declination of the sun is constantly changing between 23½° N. and 23½° S. This is given in the Nautical [Pg 80] Almanac for each two hours of Greenwich mean time with the difference for each hour given for each day. So it becomes necessary to ascertain the declination at the moment of observation, namely, at local noon. This anywhere in the Atlantic will occur subsequent to Greenwich noon, as the sun (apparently) passes around the world from the eastward to the westward once a day—24 hours—which corresponds to 360° of longitude. The rate of travel is therefore equivalent to 15° in an hour. Hence if the sun crosses Greenwich meridian and five hours later crosses the meridian of the ship, say in 75° W., the interval is 75 divided by 15, or 5 hours. During this interval the sun has changed in declination northward or southward and should be picked out of the Almanac for 5 hours Greenwich mean time.
When the zenith distance and declination are at hand the latitude is obtained by a mere algebraic addition, which is, z + d = latitude; where, if the body bears south the z is marked +, if north it is marked -; if the declination is south it is marked - and if north it is +. The result of the addition if - indicates south latitude, if + north latitude. The meridian altitude of a star, planet or moon is found in a similar manner. The formula of z + d = latitude, having regard to signs named as above, is applicable to each. The declination and the correction of the observed altitude are picked out of the Almanac and Bowditch tables in a somewhat different manner peculiar to each body.
It is found by many navigators to be more convenient to observe a body for meridian altitude by time than in waiting for the “dip.” The altitude is taken at exactly [Pg 81] local apparent noon in case of the sun and the time of meridian passage in the cases of other bodies. This expedient is especially desirable in observing stars, as the horizon is not as distinct and the “dip” not so easily detected as with the sun.
In order to secure the local mean time (L. M. T.) of a star’s transit, the G. M. T. of the star’s transit over the Greenwich meridian is found in the Nautical Almanac (p. 96) for the first day of the month and correct for the day by table on next page (N. A.). The ship’s mean time of transit will be the same, as both sun and star hold their relative positions as the star moves from Greenwich to the ship’s meridian except for the small retardation of the sun’s movement over the star’s movement. This is best found at the foot of page 2, Nautical Almanac, where the longitude in time gives the correction to be subtracted from (G. M. T.) of transit which will give the local mean time of transit at ship—the time to observe the star. An observation of a planet is similarly handled. The moon is somewhat unreliable owing to its rapid changes in position and the large corrections necessary to correct the altitude, and is consequently rather an unpopular body to observe. However, there are times when she might prove valuable in giving position when much needed.
In the case of the sun the time of transit is local apparent noon, by applying the longitude in time gives Greenwich apparent time of local noon, and corrected for equation of time gives Greenwich mean time of transit.
It is often necessary to report the latitude at noon very quickly to the master. This can be accomplished by calculating the problem to a point where the addition or [Pg 82] subtraction of the observed altitude is all that is necessary to give the latitude. The corrections are applied in advance by the estimated altitude, and declination corrected by the estimated longitude. Art. 325, Bowditch, gives the constants to be used in four different situations.
Circum- or Ex-meridian Altitude
It frequently happens, especially in the higher latitudes, that an aggravating mass of cloud drives over the sun or other objects that you are chasing, with the tangent screw, and it is lost from view together with all hope of a meridian altitude. But such an unfortunate occurrence as the loss of the mid-day latitude may be averted by employing the Circum-meridian sight or Ex-meridian, as our English cousins call it.
The mariner accustomed to its use “shoots” the sun and notes the time by chronometer or watch. Or on cloudy days, he would be standing by, near apparent noon watching for a chance to catch a glimpse of the object through a rift of cloud, and thereby forestall the loss of his latitude.
The theory of this observation is extremely simple, being merely to add to the observed altitude, taken before or after apparent noon when the sun is being considered, the amount of rise or fall between the time of sight and the time of culmination, and proceed with this amended altitude as in an ordinary meridian altitude sight.
The use of this method of obtaining the latitude is restricted to certain limits. Those who use Bowditch Tables [Pg 83] will find themselves restricted to 26 minutes from the time of transit and a declination of 63°, while Brent’s Ex-meridian Tables allow a greater scope and their limit of 70° of declination includes many stars that would be otherwise unavailable. A good guide is to never allow the number of degrees in the zenith distance to be exceeded by the number of minutes from noon. In very high altitudes circum-meridians are not to be recommended, and the higher the altitude, the more accurate must be the time used. This is plain when it is realized that the lower the sun’s altitude at noon, the more nearly its diurnal path approaches the line of the horizon; with the lessening curve of its course, comes a lessening rise near noon, hence less accuracy is needed in the exact time of sight from that of transit. In the tropics, however, where high altitudes of the sun prevail, the clouds do not offer such an element of bother as they do farther north or south, and there this problem as applied to the sun loses its popularity.
In practice the use of the tables of Bowditch makes this problem an exceedingly simple one, requiring but few figures. Table 27 contains the value of rise of the body for one minute, but as this rise varies as the square of the interval from noon, it becomes necessary to resort to another table (26) of constants for a multiplier, in lieu of the number of minutes from noon. That is, if we should multiply the amount of rise or fall for 1 minute by the number of minutes from noon, we would not be taking into account the decreasing rapidity of rise or the increasing rapidity of fall as the body approaches or leaves the meridian. But Table 26 provides a multiplier which reconciles this [Pg 84] inequality and gives the proper correction to apply to the observed altitude.
This quantity is added in every case where the upper transit is observed but subtracted when a sight is taken below the pole where the conditions are reversed.
There are several pamphlets and books on the market from which the correction to the observed altitude may be obtained. All are simple in form and with their explanations are readily understood. Notable among these Ex-meridian Tables are those by Capt. Armisted Rust, U. S. N.
The circum-meridian is a reliable method of finding the latitude, but the time used should be accurate to produce satisfactory results. If, however, the conditions be favorable, it is not necessary to discard this observation even if the correctness of the time is somewhat in doubt, for in Towson’s Ex-meridian Tables is found this note:
“If equal altitudes be taken before and after the meridian passage, half the elapsed time may be employed as the hour angle for determining the reduction. Or, when the altitudes before and after noon differ by only a few minutes, the mean of the two may be reduced by employing half the elapsed time as the hour angle for reducing the mean altitude.”
In practicing this suggestion it is necessary, in order to preserve accuracy, to put the vessel on the nearest east or west course during the run between these equal altitude observations. This is imperative in a swift vessel.
The stars and planets offer themselves for use in this problem as in all others, and here they possess special advantages of which the mariner may well avail himself. Indeed, it may be said in truth that when a horizon can [Pg 85] be obtained the latitude is always available through this problem.
And right here should be impressed upon the navigator the great advantage of becoming familiar with the stars, not merely those of greatest brilliancy, but the “lesser lights” that can be observed. Among the latter, especial acquaintance should be sought with those whose right ascensions place them in the gaps between the larger stars, thus almost the entire heavens are included in the scope of operations, making the latitude and longitude practically always available, provided again there is a horizon.
Star charts, planispheres, and globes are for sale everywhere and no study is more interesting than that of the ways of these celestial travelers. They appear and pass each day, year after year, until you consider them as old friends, and, as you come on deck for the mid-watch, you look for Orion, for instance, the same as you look for the members of your watch at their proper stations.
But we are off our course. The increasing popularity of the circum-meridian and its undoubted accuracy when used with time obtained from a carefully rated chronometer, is breaking the hold of the time-honored meridian altitude. There is no waiting with cold fingers, perhaps, for the body to dip for this sight, just shoot the star, note the time and duck for the chart room to work it up.
The most favorable position of a body for a circum-meridian altitude is one in which the rise and fall near the meridian are slow. In the case of the sun, it was explained that a low altitude proved the best, but, in the case of the stars, we find another condition; those near the pole, or in other words, of large declinations, describe such small [Pg 86] diurnal circles that here also the change in altitude is correspondingly small, thus fulfilling a desired condition for the successful working of this problem. To illustrate this point the reader is referred to Polaris. Now this star has an extremely small diurnal circle and it will be remembered that the altitude is for all practical purposes the same for a half hour either side of the meridian, showing the extreme slowness of its movement of revolution.
The stars are used in the same way as the sun except, of course, that the distance from the meridian becomes the star’s hour angle instead of local apparent time. This is readily obtained as follows: Adding to the Greenwich mean time the sidereal time of the preceding Greenwich mean noon (Nautical Almanac), together with the acceleration of Greenwich mean time (Table 9 Bowditch), gives the right ascension of the meridian. Taking the difference between this latter quantity and the right ascension of the star, we have the star’s hour angle, west, if the right ascension of the meridian is greater than that of the star, and east, if contrary conditions exist.
The circum-meridian, as well as the straight meridian altitude, is available for use of stars near the meridian below the pole, and, as one proceeds into higher latitudes, the pole becomes more and more elevated, offering thereby more opportunities for practicing this phase of the problem. The only feature to be remembered in this case is that the body is higher at the time of a circum-meridian than when it transits, so the correction to be applied to the observed altitude must be subtracted (-) in order to obtain the meridian altitude.
The planets, too, are used by the ex-meridian altitude [Pg 87] method, but being wanderers in the heavens their right ascensions and declinations must be determined for the Greenwich date from the Nautical Almanac.
The amended altitude of any body is assumed to be the meridian altitude and is used in the familiar formula z + d = latitude (see Latitude by meridian altitude); but it must be borne in mind that the result is not the latitude at noon but at the time of sight. If the observation was made say 9 minutes before noon and the latitude considered to be the position at local apparent noon as in an ordinary meridian altitude, there would be an error of 3 miles from the correct position for a 20-knot steamer.
Another point to be guarded against is that when taking several altitudes and their corresponding times their mean cannot be obtained in the ordinary way, but each altitude must be separately reduced and the mean taken of the results.
It is again necessary to diverge from the subject to impress on the mariner an urgent warning against anything but the most untiring vigilance in the care of his chronometer, and the keeping of accurate time. If this element cannot be depended upon there will be many hours of anxiety coming to him and probably sooner or later downright disaster. The almost universal establishment of time signals in all good-sized sea ports of the world together with radio time signals sent broadcast allows but little excuse for not obtaining a good rate by the time a vessel is ready for sea. Every well-known work on navigation deals with the subject of rating chronometers and so no space will here be given to it. After reading this talk on one of the most important and up-to-date observations where so much depends upon [Pg 88] the accuracy of the time, the reader cannot fail to appreciate this earnest admonishment.
Polaris
The process of finding the latitude by means of Polaris is valuable, comparatively short and the result, if the conditions are favorable, is accurate. We will consider it first in a general way.
The imaginary line representing the earth’s axis, if extended indefinitely, is presumed to pierce the celestial sphere at the celestial pole, therefore for an observer standing at our north pole this imaginary point would be exactly in the zenith and hence 90° from the horizon just as the pole is 90° from the equator, these amounts evidently bear a relation to one another. Should the person at the pole leave his frigid surroundings and proceed toward the equator, he would note that the pole had dropped lower and lower in the heavens, precisely in proportion to his progress southward, until at length, when the equator (latitude 0°) was reached, the pole would be observed to be exactly in the horizon (altitude 0°). From this it is easy to deduce the statement that the altitude of the celestial pole is equal to the latitude of the place of observation.
The object of this problem then is to obtain the altitude of the celestial pole. This point, unfortunately, is marked by no star of which a direct altitude may be observed to aid the navigator in reaching this desired result. There is, however, a star of the 2d magnitude, called Polaris (because of its proximity to the pole) with a polar distance of only [Pg 89] 1¼°. As all fixed stars are apparently revolving in circles around the celestial pole, this star joins the grand procession with its little radius of 1¼°.
It is plain that at no time can this star be more than the amount of this radius (1¼°) from the pole, and when on the meridian either above or below the pole the full amount of the radius is subtracted from or added to the corrected altitude of the star to obtain the true altitude of the pole. When the star is on a line passing through the pole and parallel to the horizon at its elongations as it is called, the altitude is then equal to the latitude, for its elevation is the same as that of the pole.
It requires 24 hours for this star to complete the small circle of revolution, the same time required by every star; its movement is necessarily very slow. By computing its hour angle, we can locate its position on this circle, and hence by applying a correction to its altitude, subtracting or adding according to the position of the star above or below the pole, we will obtain the altitude of the pole.
A rough estimate of the position of the pole may be secured by noting the position of the Big Dipper, the second star in the handle, called Mizar, is approximately in line with Polaris and the pole.
We will now proceed to show the method by which the hour angle is obtained:
In the talk on Time, it was stated that the local (astronomical) mean time plus the right ascension of the mean sun is equal to the local sidereal time; and again, that the right ascension of a star plus its hour angle equals local sidereal time. With these facts as a basis, the formula for [Pg 90] latitude by Polaris given in the Nautical Almanac will be followed in explanation.

Fig. 6.
The time of observation must be noted by chronometer and converted into local (astronomical) mean time; this must be corrected by Table III (Nautical Almanac) in order to change this solar interval into a sidereal time [Pg 91] interval; to this converted time must be added the Greenwich sidereal time of mean noon (page 2); that is, the hour angle of the First Point of Aries, or what is the same thing, the right ascension of the mean sun; to this sum must be applied a correction for longitude, in time, taken from the foot of page 2, N. A. The sum is the local sidereal time.
The reason for the correction of longitude is this: The difference between the right ascension of the mean sun at noon on two successive days is 3 m. 56 s., the same as the accumulated difference between solar and sidereal time in 1 day. Now we take from the Nautical Almanac this element for Greenwich mean noon, yet the sun has since covered the distance equal to the longitude, and during the interval required to do this, the sidereal time has accelerated over the solar an amount which bears the same ratio to the 3 m. 56 s., that the longitude in time bears to 24 hours. The Nautical Almanac handles the terms of this proportion in tabular form at the foot of page 2. It is stated that the sun has traveled from the meridian of Greenwich to the local meridian, and it might be suggested that at the time of observation the sun has covered this amount plus the local hour angle or the local astronomical mean time. This is true but the amount of local hour angle has been previously accelerated to sidereal time by the correction to local astronomical mean time.
With the local sidereal time enter Table I (Nautical Almanac) and pick out the correction to be applied according to sign to the altitude. It is probably needless to say that the observed altitude must be corrected for index [Pg 92] error, dip and refraction before applying this latter correction, which converts it into latitude.
This is called the Nautical Almanac method and is sufficiently accurate for navigational purposes, but should a greater refinement be desired there are tables of further corrections given in the American Ephemeris and Nautical Almanac.
It is always advantageous to get an observation of a star near twilight or dawn, in order that a well-defined horizon may be available; but, in taking a sight of Polaris, another important feature is to be considered. When the star’s hour angle is at or near 6 or 18 hours, that is, near that part of its orbit cut by a line passing through the pole and parallel to the horizon, it is rising or falling most rapidly, with the result that a small error in time will produce a considerable error in the hour angle, an error of 3 minutes introducing a difference of 1´ in the latitude.
It is quite worth while, therefore, to select a time for the observation of Polaris when this star is near either of its culminations, its highest or lowest positions, where the time need not be especially accurate; but by carefully noting the time it is possible to get good results at other times when the horizon is defined. By using the position of the star Mizar, as suggested above, however, the navigator will be greatly aided in selecting the most propitious time for observing Polaris.
Of all the navigational instruments now in practical use, there are few, if any, that exceed the mariner’s compass in usefulness to mankind. The part it has played in the development of the world has been most important, and its utility is no less to-day than in the past, for the intercourse of nations is still guided by the compass needle. With such a responsibility depending on this instrument, it would naturally be supposed that its indications must be very accurate, but, on the contrary, the needle is swayed by the slightest magnetic influence and points North only on rare occasions; and in steel vessels only by mere chance.
The needle is drawn from true north first by the direction of the earth’s magnetic force which is not coincident with the meridian owing to the position of the magnetic poles. The north magnetic pole being in the extreme northern part of Canada, all the lines of force in the northern hemisphere converge toward this locality. The needle when otherwise undisturbed lies in the direction of these lines of force and takes an angle with the meridian depending on the locality.
The amount of divergence from the true north, or variation, as it is called, differs in different localities but is readily [Pg 94] obtained by a glance at the chart where each compass rose shows the amount of variation at that place. From a magnetic course, or bearing, the true course, or bearing, is readily found by the proper application of this variation, which may be either easterly or westerly. The true course is to the right of the magnetic course, when considered from the center of the compass, in easterly variation; T. R. E.—True-Right-Easterly. Remember these three words and the whole lesson is learned, for if true is to the right in easterly variation it must be to the left in westerly; and if true is to the right in easterly, the magnetic course must be to the left of true course in easterly and to the right in westerly. In this way the true and magnetic courses are converted one to the other at will.
If we were to sail always in an entirely wooden ship, our compass troubles would be very few, for the above would include every phase of the situation. As wood is non-magnetic the compass would be uninfluenced by outside disturbances. Wood, as a ship-building material, having been so much displaced by iron and steel, the use of these metals has brought many problems to solve in connection with the deflection of the compass needle.
The effect on the compass needle of the magnetism in a vessel and her cargo is known as deviation and is very complicated, owing to many influences which are at work at all times giving an ever-varying value to this element of error.
The causes of deviation and its treatment in the way of compensating the compass are subjects much too extensive for this little book; furthermore, they are carefully dealt with in a half dozen of the well-known works on navigation, [Pg 95] so we will touch only on the every-day side of compass work.
The deviation changes with every alteration of the vessel’s head, owing to the change in position of prominent parts of the vessel’s hull relative to each other, to the compass, and to the terrestrial lines of force (magnetism).
As a result of these influences on the compass needle, the mariner has three courses to deal with. The first is the true course, which is based on a compass whose needle points true north. The second, the magnetic course, is taken from a compass affected by variation alone and therefore pointing to the magnetic pole. The third is the compass course, or that course actually shown by an ordinary standard compass in a steel ship, affected by the error of variation combined with the error of deviation.
The combination of the deviation and the variation is the compass error and is obtained by adding the deviation and variation if both are of the same name, the compass error taking that name; for instance suppose we have a variation of 2° W. and deviation of 10° W., the combined error is 12° W. If, however, the variation and deviation are of different names, it becomes necessary to find the difference between the two and name the result after the greater quantity; thus, with a deviation of 4° E. and a variation of 10° W., the error is 6° W.
The compass error is applied to compass course to obtain true course and vice versa by the same rule as for variation.
The navigator in planning his course between two positions lays the parallel rulers on these positions on the chart and carries this direction to the nearest compass [Pg 96] rose. This may be a true rose, in which event he remembers his T. R. E. rule, reversing it in this case, and with the variation given on the chart secures the magnetic course. In an iron or steel vessel, the deviation for that course must be ascertained from the deviation card by trial or from a Napier Diagram direct and applied to the magnetic course in order to obtain the compass course. This is accomplished precisely as in finding the magnetic from the true course (to the left if deviation is easterly and to the right if westerly). The course by standard compass is now at hand by which we can steam from one selected point to the other.
The deviation as has been said is an ever-varying error, and consequently it is quite impracticable to depend wholly on a fixed deviation card. We may take aboard some magnetic cargo or change our latitude to a great extent, the vessel may be pounded excessively by heavy seas, a stroke of lightning or by stranding; all these are causes liable to affect the deviation more or less.
In order to forestall the serious consequences that are liable to attend such a derangement of the normal and expected deviation, the careful navigator takes azimuths or amplitudes on every course when practicable. Azimuths and amplitudes are nothing more nor less than astronomical bearings of heavenly bodies; they indicate the true bearing of the body, and the difference between this bearing and the bearing taken simultaneously by standard compass is the compass error.
The azimuth of a body is the angle at the zenith between the meridian and the vertical circle passing through the body. It is customary, however, to consider the [Pg 97] azimuth as measured by the arc of the horizon rather than by the angle at the zenith. It is measured from the north or south point according to the latitude, toward either the east or west point, through 180°.
An amplitude, unlike an azimuth, is restricted as to time of observation, for the body must be on the horizon either rising or setting; and should be observed when the sun is about its own diameter above the horizon and with a not excessive height of eye. The amplitude is measured from the east or west point through 90° to the north or south point. If the body observed has a south declination and is rising, the amplitude will be East so much South; if declination is north, East so much North, for a body rises in the East point when its declination is 0°—on the equator.
The principle of the amplitude lies in the solution of a right-angled spherical triangle, whose sides are the body’s polar distance, the co-latitude, and the zenith distance which is 90°. We desire the complement of the angle at the zenith. It is unnecessary to compute an amplitude, for in Table 39, Bowditch, will be found the desired bearings for different latitudes and declinations. The sun will be found the most satisfactory of the heavenly bodies to utilize for amplitudes.
There are two methods of calculating an azimuth, one known as the time azimuth and the other as the altitude azimuth. The former is the most popular owing to the tables that have been compiled, an inspection of which facilitates the navigator in quickly obtaining the true azimuth of a body. Before entering the tables, it is necessary to have as arguments the latitude and declination, [Pg 98] and, if using the sun, the local apparent time, or for stellar work the hour angle. Should the star’s hour angle exceed 12 hours, 12 hours should be subtracted from it, and the remainder used as P.M. time. A planet may be employed precisely in the same manner as a star.
One of the simplest and most expeditious methods of securing the azimuth is by means of a diagram. Upon this convenient invention the bearing of a body can very quickly be taken off with a pair of rulers. Weir’s Azimuth Diagram is sold by the Hydrographic Office for a very small sum. The only argument that can be used against its use is that it requires a small table to lay it upon. Simple and complete directions are printed on the diagram.
The altitude azimuth is often computed at the same time as the ordinary A.M. and P.M. time sights, utilizing the altitude of the body for both operations. The principle involved in computing both an altitude azimuth and a time azimuth is the solution of the same astronomical triangle for the same angle, but in the case of the altitude azimuth three sides are given (the co-latitude, the zenith distance, and polar distance) to find the angle at the zenith. In the time azimuth, two sides and the included angle are given (the polar distance, co-latitude and local apparent time or hour angle) to find also, the angle at the zenith.
The azimuth found by computation should be named North if in north latitude, or South if in south latitude.
It has been customary to add up the logs, divide by 2 and the cosine will be half the azimuth named from the elevated pole, but a more expeditious way is after adding the logs seek in the log haversines and find the azimuth directly but named from the opposite pole to the latitude.
[Pg 99] With the correct bearing of the sun, and its simultaneous bearing by standard compass at hand, the compass error is found by merely taking their difference. Now this error, as said before, is composed of the sum or difference of the deviation and the variation, so, if either is subtracted from their sum, or added to their difference the remainder is the other quantity. The variation being always known is subtracted from or added to the compass error to obtain the deviation, thus checking the deviation card for that particular course the vessel was steering at the time of observation.
With the compass error at hand, many students become perplexed as to the proper manner of dealing with this error, and finding from it the deviation. The compass error is first named, by considering the two bearings (compass and true) from the center of the compass; if the true is to the right of the compass bearing, the error is easterly, if to the left, westerly.
Now should the variation happen to be identical with the compass error, both in amount and in name, there is no deviation; if the variation is 0°, then the whole error is deviation. If by chance the compass error is 0°, it indicates that the variation and deviation are equal in amount and opposed to each other in their influence on the needle. The deviation, in such a case, naturally takes the opposite name from the variation.
In separating the variation from the compass error, it is necessary to exercise a little thought and to consider what deviation applied to the given variation will produce that compass error. This will be readily seen after a little practice. There are, however, some rules which are here [Pg 100] given, by which the deviation can be obtained mechanically.
The deviation is the difference between the variation and the compass error if they are of the same name or adding them if of different names. It is given the same name as the compass error unless the compass error is subtracted from the variation, when the deviation takes the opposite name.
Or a diagram in which the error is shown by its particular number of degrees east or west of the true north line may be drawn and the variation likewise properly shown east or west of true north. If the error is to the left of the variation the deviation is west and if to the right the deviation is east.
The longitude of any position on the earth is its distance east or west from the meridian of Greenwich, which has been chosen as the meridian of origin. Longitude is measured on the equator eastward and westward through 180°, completing in this way the whole circumference of the earth.
The circumference of every circle comprises 360°, whether it is a great circle of the earth or any of the parallels which range in size from a point at the poles to a great circle at the equator. There are always 360° but the length of each degree is determined by the size of the circle. Thus a degree of longitude on the equator is 60 miles, while on the 50th parallel of latitude it is only about 39 miles, owing to the decreasing size of the parallels of latitude. A minute of longitude on the equator, like a minute of latitude, is equal to one mile, but the difference between the meridians in actual distance decreases toward the poles gradually lessening the linear value of a degree of longitude. Thus it will be seen that when it is desired to represent a difference of longitude in distance, it must be done in terms of departure (miles) corresponding to the particular parallel of latitude of the position.
The sun apparently moves around the earth in its diurnal motion, covering 360° in 24 hours, whether the declination [Pg 102] is north or south, and a little simple division shows that in one hour he passes over 15° of longitude, whatever the latitude. This reduced shows that 1° is passed over every 4 minutes. As the standard time, the world over, is reckoned by the movements of the sun, it is plainly seen that when considering longitude, a definite relation exists between time and arc (°-´-´´). Owing to this relation, time and arc become interchangeable by a simple process of conversion.
So it follows that if we have the time at Greenwich by a chronometer, and through a trigonometrical calculation we determine the local mean time at the ship, the difference in time between Greenwich and the ship’s meridian represents the longitude in time, which is readily converted into arc.
The calculation involved in determining the local mean time is the solution of the astronomical triangle, or in other words it is a problem in spherical trigonometry. This triangle has its apex at the pole with one side as the polar distance (90° - declination of the observed body), another side the co-latitude (90° - dead reckoning latitude) and the third side the zenith distance (90° - the corrected altitude of the body).
It is one of the principles of trigonometry that with any three elements given in a triangle any of the remaining elements may be computed; that is, any angle or side is obtainable. The solution of the astronomical triangle for various elements includes the finding of the zenith distance and from this the altitude, which forms the main feature of the problem involved in the New Navigation. It also provides us with the angle between co-latitude and the [Pg 103] zenith distance, which is the azimuth of the body, by which the mariner is able to ascertain the error of his compass.
The most important feature of the astronomical triangle is the angle at the pole, known as the hour angle, which when found secures for the navigator his local time. The problem presents itself in the form of three sides being given to find one angle. It is found by the time sight formula, which is too well-known to need any discussion here.
The shape of the triangle is determined by the declination of the body, its altitude and the latitude of the vessel, and the polar or hour angle; and it stands to reason that a formula will not produce the same accuracy in the hour angle with every shape of the triangle. For instance, in high latitudes or when the body has a declination approaching 90°, the accuracy of the time sight formula becomes effected.
Another very important point to bear in mind when observing a body with the view of computing its hour angle, is its azimuth. When the bearing is nearly east or west, on the prime vertical, the body is rising or falling faster than at any other time, and an error in altitude or latitude will produce the least error in the resulting longitude. The necessity for close attention to this point is increased with the latitude. Observations for time taken when the body has an azimuth of less than 45° or over 135° are wholly unreliable.
The sun does not always cross the prime vertical in his daily track across the heavens, for under certain conditions, say during the northern winter, he will rise southward of east and set southward of west. Under these adverse conditions, [Pg 104] the calculation of longitude is not dependable, and the best a navigator can do when using the sun is to observe as soon as he has an altitude sufficient to clear the excess refraction existing near the horizon.
It is under such circumstances that star sights are of incalculable value, for a star can always be found in a suitable position with but little waiting, or we may employ the New Navigation method, where the azimuth of the sun is as good one place as another.
In order that a body will cross the prime vertical, the latitude must be of the same name and greater than the declination. In conditions cited above the declination of the sun is south and the latitude is north, hence the body will never be on the prime vertical. If the latitude is less than the declination, the sun’s diurnal track is tilted toward the zenith, instead of away from it as when the latitude is greater, and the result is that the sun, while never on the prime vertical, approaches it for a time after rising, then recedes again. It should be observed when at its nearest point to the bearing of east of west.
The bearing of various bodies can be readily found by an inspection of Hydrographic Office Azimuth Tables Nos. 71 and 120, the declination and latitude being used as arguments.
There is a method of finding the longitude known as the equal altitude method, but it is not valuable. The conditions are exacting where accurate results are required and when these conditions exist the ordinary time sight is available and at its best advantage, so longitude by equal altitudes is not popular. To secure good results, the body must have an altitude above 70° and near the prime [Pg 105] vertical; and, furthermore, the ship must be kept on an east or west course or remain stationary. The theory of the problem is simplicity itself, and for this reason is very alluring, but the best use that equal altitudes can be put to is the determination of chronometer error ashore, and in these days of radio time signals even this use is almost obsolete. The rule is as follows: Observe the sun’s altitude, simultaneously noticing the time by chronometer and clamp the sextant to prevent any chance of the altitude becoming disturbed. When the sun has fallen to the same altitude as of the forenoon sight, note the time again by the chronometer. The mean of the two times, corrected for chronometer error, equation of time, and the equation of equal altitudes due to change in declination, in case of the sun, is the Greenwich apparent time corresponding to our local noon or our longitude in time, which should then be converted into arc.
The stars and planets are available as well as the sun for the finding of longitude and when there is a distinct horizon, stellar sights have many advantages. The problem depends upon the solution of the astronomical triangle by the same formula as with the sun.
There are a few points of difference between a time sight of the sun and one of a star or planet needing explanation. In the case of the former body, we naturally compare the solar time of Greenwich with the solar time of the local meridian, but in stellar work we employ for this comparison stellar time, or, as it is more popularly called, sidereal time. So it becomes necessary to turn the Greenwich mean time of the chronometer into Greenwich sidereal time and compare it with local sidereal time. The difference, as in mean [Pg 106] time, is the longitude in time, which is converted into arc in precisely the same way.
The Greenwich mean time is turned into sidereal time by adding to it the right ascension of the mean sun, taken from the Nautical Almanac and the acceleration for the Greenwich mean time (Table 9, Bowditch). The local sidereal time is the result of an addition of the star’s right ascension and the star’s hour angle, the right ascension is taken from the Nautical Almanac without correction if a fixed star is being considered and the computation of a time sight gives the star’s hour angle. The local sidereal time being the right ascension of the meridian, it follows that the angle from the vernal equinox to the star plus the angle from the star to the meridian is what we desire; hence the above rule for obtaining the local sidereal time.
Should the star bear east of the meridian, the local sidereal time may be found by subtracting the (easterly) hour angle from the star’s right ascension or adding them as above and subtracting 24 hours. Reference to the Time Diagram, Fig. 3, will make these points clear also.
It is customary to add up the familiar logs of time sight—sec. lat., cosec. p. d., cos ½ sum, sin, remainder—divide by 2 and seek the H. A. (hour angle) in the A.M. or P.M. column of Table 44, Bowditch, using the log as a sin; but a more expeditious way is to use the sum of the logs as the log haversine in Table 45 and pick out the hour angle directly.
Every mariner who has reached a position in the profession where he is intrusted with the responsibilities of navigating a vessel is under obligation to the late Capt. Thomas H. Sumner, of Boston. This shipmaster discovered and developed the principle of the so-called Sumner or Position Lines, a principle which has proved of inestimable value and which, with its subsequent improvements, has well-nigh revolutionized the methods of navigation.
The discovery was purely accidental and for that reason is interesting. Here, in Capt. Sumner’s own words, is how it occurred: “Having sailed from Charleston, S. C., 25th November, 1837, bound for Greenock, a series of heavy gales from the westward promised a quick passage. After passing the Azores, the wind prevailed from the southward, with thick weather, after passing longitude 21° W., no observation was had until near the land, but soundings were had not far, as was supposed, from the edge of the bank. The weather was now more boisterous, and very thick, and the wind still southerly.
“Arriving about midnight, 17th December, within 40´ by dead reckoning, of Tuskar light, the wind hauled S.E. (true), making the Irish coast a lee shore. The ship was then kept close to the wind and several tacks made to [Pg 108] preserve her position as nearly as possible until daylight, when, nothing being in sight, she was kept on E.N.E. under short sail, with heavy gales. At about 10 A.M. an altitude of the sun was observed, and chronometer time noted; but having run so far without any observation, it was evident that the latitude by dead reckoning was liable to error and could not be entirely relied upon.
“However, the longitude by chronometer was determined, using the uncertain D. R. latitude, and the ship’s position fixed in accordance. A second latitude was then assumed 10´ to the north of the last and working with this latitude a second position of the ship was obtained and again a third position by means of a third latitude still 10´ further north.
“On picking off these three positions on the chart it was discovered that the three points were all disposed in a straight line lying E.N.E. and W.S.W., and that when this line was produced on the first-named direction it also passed through the Smalls Light. The conclusion arrived at was that the observed altitude must have happened at all three points, at the Smalls Light, and at the ship at the same instant of time. The deduction followed that, though the absolute position of the ship was doubtful, yet the true bearing of the Smalls Light was certain, provided the chronometer was correct. The ship was therefore kept on her course, E.N.E. and in less than an hour the Smalls Light was made bearing E. by N. ½N. and close aboard. The latitude by D. R. turned out to be 8´ in error.”
If the captain had worked more time sights using different latitudes, he would have added new positions on the line to which he refers, each placed upon it according to the [Pg 109] latitude used. Had he cared to pursue his experiments farther, and used latitudes very wide of his dead reckoning position, he would have discovered that the resulting positions instead of lying in a straight line, were in a curve and an arc of a circle.
The principle involved is very crudely illustrated in the following experiment: Let the reader consider himself aboard ship lying at anchor—say a full-rigged ship, so as to insure a foremast of good height. Lower the dinghy and take along a sextant.
We start with a series of measurements to determine the angle, as read from the sextant in the dinghy, between the truck and the waterline about the vessel. As a result of these measurements, we discover that this angle becomes smaller as the distance from the vessel increases.
Carrying our tests farther, suppose when the sextant shows the altitude of the fore truck above the waterline to be 70°, that the distance to the vessel be determined. With this distance as a radius and the foremast as the center, we row in a circle around the vessel, the sextant will continue to read 70° all around the circle.
It is thus demonstrated that a circle surrounds that foremast upon which the altitude of its truck is everywhere 70°—a circle of equal altitudes.
Not being quite sure of this interesting fact, perhaps, another angle is selected by moving a little farther from the ship. The sextant shows the fore truck to have an altitude of 50°; the distance to the vessel is established, whereupon the dinghy is rowed around the vessel with this distance as a radius. Again the sextant reveals no change from 50° [Pg 110] and it is clearly shown that we have moved about on a circle of 50° elevation of the truck.
We can continue experimenting in this way until the distance from the ship becomes so great that some physical condition prevents our reading the angle of the truck’s altitude.
These investigations show that there is a system of concentric circles of equal altitude about every elevated object like the little undulations we have seen so many times produced by the splash of a stone thrown into a pool.
These circles of equal altitudes surround not only elevated terrestrial objects but also celestial bodies, as will now be shown. As the sun is the most convenient body for this illustration, let us substitute it for the fore truck of the foregoing experiments, while for the waterline of the vessel we will use the point on the earth touched by a plumb-bob suspended from the center of the sun.
This point will fall on the equator on the 21st of March or thereabouts, as the sun coming up from his southern declination crosses the equator into north declination at this time. The instant of the transit is the vernal equinox. Now this point will be found an excellent one from which to study this problem, but, as this takes some time and the sun is ever on the move, we will imagine ourselves endowed with the power of Joshua to command the sun and moon, which will enable us to study this phenomenon while free from the restlessness of the Universe.
First of all, it must be understood that the sun shines on one hemisphere of the earth at all times; it matters not how the earth is tipped in relation to him, one half of the world is always enjoying sunshine. The center of the [Pg 111] lighted area is the spot directly beneath the sun where the plumb-bob touches and about this point lies the system of concentric circles of equal altitudes of the sun.
Under the conditions shown above, the sun is in the zenith of the terrestrial vernal equinox, shining on the earth for a distance of 90° in every direction; but its altitude diminishes in direct proportion with the distance of the observer from the point of the equinox. On the great circle everywhere 90° from the equinox the sun is in the horizon with an altitude of 0° (provided we disregard dip and refraction). Suppose the members of some intrepid expedition have reached the northern or southern pole; they would, at the time being considered, see the sun in the horizon and in the direction of the meridian passing through the vernal equinox.
Eastward along the equator 90° of longitude from the vernal equinox, the inhabitants are just resting from the toils of the day, for with them the sun is setting in their western horizon, while away to the westward 90° the people are showing signs of activity, for it is just sun-up in their eastern horizon.
So all around the world just 90° from this selected position and at this appointed time is a circle of equal altitudes, namely 0°, for is not the sun seen in the horizon at all points on this circle?
The altitude of the sun is 90° at the point of observation and 0° on its outer circle of altitude; these are the two extremes and between them lies an infinite number of concentric circles of equal altitude for navigators to utilize. The zenith distance, derived by subtracting the altitude from 90°, indicates the distance of each circle from the [Pg 112] center or sun’s position. Thus if an observation was taken by some bewildered mariner in which the altitude was found to be 80°, the corresponding zenith distance of 10° multiplied by 60 would indicate that the altitude was taken 600 miles from the sun’s position, or to put it in another way, the circle of equal altitudes upon which the observer was located in this case had a radius of 600 miles.
What is true of the sun on the equator regarding the principle of the circles of equal altitudes holds good throughout its range of declination, the whole system moving north and south with the continuous change of declination and from east to west with its apparent diurnal motion.
In the quoted article, Capt. Sumner shows a method by which the position of a vessel may be established on some particular circle of equal altitude; it matters not where the observed body happens to be at the time, for with the Nautical Almanac and chronometer it can be located should we care to know. The navigator, however, cares to deal ordinarily only with a very small arc of the circle embraced within his immediate whereabouts. Should he be somewhat uncertain of these he would simply require the use of a longer line to extend beyond the limits of his possible position.
Except when in a latitude that differs but little from the declination of the observed body, the circle of equal altitude will be sufficiently large to allow the mariner to represent its arc in his vicinity by a straight line. Thus the lines of position used to plot a vessel’s position on the chart are in reality chords or tangents of the circle of equal altitude. In geometry it will be remembered that we used to study about circumscribed and inscribed polygons [Pg 113] and here we have a practical application of their use. If we consider the line of position to be a tangent, it is one side of a great polygon with a vast number of sides circumscribed about the circle of equal altitude; and if we consider it to be a chord, it is likewise a side of a great polygon inscribed within the circle of equal altitude. It matters not, however, if the line or curve of position is considered a straight line, except in the ill-chosen condition of the body near the zenith when the radius of the circle will be proportionately small. If exactly in the zenith there will be no circle of equal altitude at all and the sextant will measure an altitude of 90°. It is comparatively rare, however, that such a condition will embarrass the use of this method.
Another point to be remembered in connection with the inscribed and circumscribed polygon propositions and one which has a practical application in the use of position lines, is that the tangent or chord of a circle is at right angles to the radius passing through the point of tangency or center of the chord. It follows that the sub-celestial or terrestrial position of the observed body, being at the center of the circle, is always at right angles to a line of position.
This important fact gives the navigator an opportunity to check his compass error each time he establishes a position line, by comparing a compass bearing of the body taken simultaneously with the measurement of the altitude, with the true bearing.
To establish a position line as Capt. Sumner did and as it was done for years afterwards, by assuming two latitudes usually 10´ each side of the dead reckoning latitude, and drawing the line through the two resulting longitudes, is known as the chord method. The two longitudes being [Pg 114] positions on the circle a line drawn between them is a chord of the circle.
The work of computing a time sight is more or less laborious to everyone and with some seafarers forms their most arduous mental exercise. At any rate no one wants to work any more than is necessary to insure accurate results. So when establishing a position line it will often be found convenient to use the short cut known as the tangent method.
With the latitude by account work the observed altitude as in the ordinary time sight, instead of assuming two latitudes. Seek the true azimuth in the tables or on diagram, using the latitude and declination employed in the time sight and the local apparent time gained from it, as the arguments. The true azimuth, it will be remembered, always bears at right angles to the position line. Hence if the azimuth is laid down through the position furnished by the time sight, the position line may also be readily plotted at right angles to the line of azimuth at the time sight position.
The navigator now-a-days is expected to think in position lines when he is clear of the land, as a pilot thinks in shore bearings and marks. That is, he must see these imaginary lines of the different visible bodies, and keep track of their availibility for his particular use. It is easy to get into the habit of this, for they are simply astronomical bearings instead of bearings on distant terrestrial objects, with the distinction that the celestial bearing allows of a 90° correction to produce a position line.
The morning sun on the prime vertical with a sufficient [Pg 115] altitude to avoid any dangerous refraction, will produce a north and south line of position. During the forenoon as the sun passes toward the meridian, the northern end of the position line will move in direct proportion with the body’s change in azimuth to the eastward and the southern end to the westward, until at noon with the sun on the meridian we have an east and west position line.
It will be seen that at one moment of the day it is a very easy matter to establish a line of position; the mere working of a meridian altitude does this. This simple expedient of finding a position line was utilized a great deal as a means of making a landfall in the days before chronometers were perfected. In those good old days, before the clipper ship era, time was not held at such a premium as in the present hustling period, and a few days more or less at sea mattered but little. The shrewd shipmasters then would keep well offshore until in the latitude of Boston or the Virginia capes, as the case might be, when they would haul due west and let her go, making, no doubt, first rate landfalls, if the old pig yoke was in good working order.
The value of a position line was demonstrated to the writer some years ago when bound in from the eastward and running into a heavy and very extensive fog bank somewhere southeastward of Halifax. During a break in the prevailing conditions the navigator succeeded in securing an ex-meridian sight and fortunately got a fairly good idea of the latitude. The vessel was under sail and making but slow progress, and as a result of the protracted period of overcast sky the longitude became considerably a matter of guess work. The vessel, however, was kept on a west course with a careful allowance made [Pg 116] for the set. “Sir William Thompson” was kept going at regular intervals and it was surprising to see the soundings check up with the chart as the vessel approached, crossed, and left astern the Roseway Bank, southward of Cape Sable. One felt as sure of the position as did the old Nantucket sailor in crossing “Marm Hackett’s garden.”
In cases where the soundings do not check so precisely as in this instance, it will sometimes be found a great help to lay off to scale the depths obtained on the edge of a piece of draftman’s transparent linen. Place it on the chart in the line of the course, and, should the soundings fail to agree, move the scale forward and back or to either side, always preserving the direction of the course, until a position is found where the soundings on the scale agree with the depths given by the chart.
Progress has been made in the science of navigation as in all other sciences, and the modern shipmaster is not obliged to hold aloof from Nantucket Shoals and Georges Bank under ordinary conditions as our ancestors were compelled to do, for with a correct chronometer and a knowledge of the position line such outlying dangers have been robbed of many of their anxiety-producing elements. Before showing the method of working around such places another point of value of the position line is called to the reader’s attention.
A line of position extended until it reaches the land or some danger will indicate to the mariner the bearing of that particular point of the coast or danger. If it so happens that this point is not the place of destination, the navigator, not being able to lay a course direct for his objective port through inability to determine the vessel’s distance offshore, [Pg 117] overcomes the difficulty by sailing a sufficient distance at right angles, then hauling on to a new position line parallel to the original one. This is similar to what our ancestors did in the simple way cited above. If the line lies in the direction of an off-lying or isolated shoal that is dangerously near the course, an offset like that shown above will allow a course parallel to the position line to be sailed in safety. Here is an example to show its useful application:
A steamer sailing from St. John, N. B., for New York proceeded but about 10 hours on her voyage, when she ran into a terrific gale. The master was soon forced to heave his vessel to and ride it out as best he could. The driving snow and mountainous seas occupied the attention of the officers in their efforts to save the steamer and in this way the dead reckoning position became a matter of mere guesswork. The wind after some 20 hours in the northeast quadrant hauled to the northward, at length blowing out in the northwest with clearing weather.
It was the master’s intention to pass through the South Channel, between Georges Bank and Nantucket Shoals, but as he had lost his reckoning to such an extent he hesitated about laying a course through such a danger-strewn locality.
In the late twilight immediately following the clearing sky, the master succeeded in catching the altitude of a star bearing 300° and established a line, the direction of which led close westward of Cultivator Shoal (a 6-foot spot on Georges Bank). So to be on the side of prudence and give this shoal a good berth, the master steamed 8 miles at right angles to this position line. The course or direction of the new position parallel to the first was found to lead [Pg 118] directly into the range of visibility of Nantucket Lightship. So the master’s mind was put at rest as he laid his course along the second position line, knowing he would at length make the lightship.
It often happens that a distant mountain peak is visible and the sun is in a suitable position to establish a set of cross bearings, using the mountain for one object and the sun for the other. Now with what has previously been stated, it is hardly necessary to remind the reader that a “line of position” obtained from observations of the sun will be at right angles to the sun’s true bearing; therefore, in order to judge whether these objects are properly placed to give a good intersection, due consideration must be given to the relative bearings of the objects. It is evident that the sun must bear by compass nearly in the direction of the mountain or in the opposite direction to have the position line and the line of bearing of the mountain cut at nearly right angles. Of course, as with any set of cross bearings the angle of intersection may still be effectual if the lines cut at 50° to 60°, but the nearer a 90° cut the more accurate the resulting position.
A position line is liable to displacement through a variety of causes among which is an inaccurate altitude and through incorrect Greenwich mean time. In the former instance, an error of 1´ will displace the position one mile; if the altitude is 1´ too large, the correct position of the line will be 1 mile directly away from the bearing of the body and vice versa. The effect of an error in time upon a position line is to displace it bodily eastward or westward the amount of arc corresponding to the error in the chronometer; the direction of the line is, however, unaltered. [Pg 119] The sun carries his system of circles of equal altitude with him from east to west as he travels along a certain parallel of latitude corresponding to his declination (neglecting the slight change in declination). It is quite evident that any arc of a selected circle, will, if its position is plotted on a small scale chart—say every 20 minutes—be found continuously parallel with itself. And the intervals between each two plotted positions of the arc will be 5° (of arc) the corresponding value of 20 minutes. Thus the displacement of the position line due to an error of time is explained. If the time was slow, the line was too far to the eastward, if fast, it was too far to the westward.
The value of a position line has been demonstrated, yet with all it does not positively establish the position of a vessel. The mariner in locating his vessel in a harbor does not usually stop after he has taken one bearing, but proceeds to find another object whose bearing will make a favorable “cut” with the first, and thus at their intersection determines his position. As a further check against possible error a third object may be chosen and, if the three bearings plot without forming a triangle at their intersection, a very reliable fix will be obtained.
What applies to terrestrial objects thus employed may be used as an illustration to be followed in taking celestial bearings. If the mariner establishes a position line and knows his vessel is located at a point somewhere along it, let him look about for another body so placed that the position line derived from it will make a good intersection with the first line; if all data are correct this point will indicate the position of the vessel.
When the sun is used this is seldom possible but in lieu [Pg 120] of another body the sun can again be employed to establish the second position line after it has moved sufficiently in azimuth to make a good cut. The thought no doubt immediately arises as to the effect of the vessel’s change in position during the interval. This is easily taken care of by means of the course and distance run during the interval between the sights.
The first position line must be considered carried bodily by the vessel without change of bearing from its first position to the position of the second observation. That is, if at 9 A.M. a position line was established bearing in a 15°-195° direction, and the vessel then steamed and made good a 40°-course for 6 hours and 10 knots an hour, when another position line was established, the 15°-195° line of 9 A.M. would be moved bodily in a 40° direction 60 miles; where its intersection with the second line would indicate the position of the vessel at 3 P.M. The determination of position at sea by employing two position lines of a body with the run between sights is called Sumner’s double altitude problem.
It has already been shown that one body, notably the sun, can be used to get an intersection of two of its lines of position by waiting a sufficient time between observations for the body to change its bearing at least 30°, the nearer 90° the better. The relationship between the interval of time and the amount of change of bearing varies greatly, depending upon the latitude of the observer and declination of the body. For example, let us consider the two extreme cases: Suppose a mariner to be observing the sun on the equator on March 21st, he will note practically no change in azimuth during the whole forenoon. Yet [Pg 121] another mariner in the Polar sea, whose latitude differs about 90° from that of the former, will have the sun encircling his horizon making the whole amount of the sun’s movement a corresponding change in azimuth.
Therefore it will be seen that with a low-riding sun (or other body) the change of azimuth is greater in a given time, and for this reason the position lines derived from the sun are more advantageously practiced in higher latitudes, especially in winter. This is a point of great value in view of the fact that the sun’s diurnal course is such that it is never on the prime vertical in northern latitudes during the winter months, making longitudes derived from chronometer sights very unreliable.
But to go back to the mariner on the equator whose latitude and sun’s declination so nearly agree. He is in a predicament should he persist in the plan to determine his whereabouts by position lines of the sun. In such an unusual case, it would be well to resort to some other method or wait until evening and determine the ship’s position by establishing the position line of some star or stars. It will be but a few days before the ship’s progress will cause the sun to leave his right course across the sky and take the hour circles at an angle. Take a case when the sun at noon has a zenith distance of 10°, the change of azimuth during the forenoon is still small, but suppose the bearing was noted 1 hour, or even less, before noon and again in similar amount after noon, a change will be found of perhaps 90°, the difference of moving from the southeast quadrant (if declination is south of latitude) to the southwest quadrant. In this way, a remarkably good cut may be had within a comparatively short time.
[Pg 122] The foregoing will convince the reader that he must be governed by the change of bearing and not by time elapsed, in predicting the value of the cut of his position lines.
In the use of position lines, it is necessary to bear in mind, that, when the body’s altitude begins to approach the zenith, or, what is the same thing, when the ship is getting close to the body’s sub-celestial position, the circle is getting proportionately smaller. Under such conditions the arcs of the circle of equal altitudes can no longer be shown as a straight line. The double altitude as it is ordinarily practiced is here impracticable. And even outside this impracticable area, discretion must be shown. The dead reckoning position must be proportionately accurate, and the assumed latitudes must be brought correspondingly close together, in order to have a shorter line of position, because the curvature of the circle is getting sharper as the sub-celestial point is approached. To put it in another way, a smaller arc must be used in order to avoid the error due to excessive curvature.
Very good results can be obtained by noting the time of observation by chronometer (G. M. T.) and correcting it for equation of time in order to get Greenwich apparent time. This, if converted into arc, is the longitude of the sub-solar position. By using the Greenwich mean time to correct the declination taken from the Nautical Almanac for that day, the latitude of the sub-solar position may be obtained. Plot this position on the chart and use it as the center of a circle; then with the zenith distance (90° - altitude) as a radius, draw an arc in the probable position of the vessel. Somewhere along this arc is the ship’s position. The bearing of the sun (rather hard to get so [Pg 123] nearly overhead) corrected for compass error, reversed, and laid off from the sub-solar position will give a fair idea of the position of the vessel. Now by waiting a sufficient time for the sun to change its azimuth enough to make a good cut and using its new sub-solar position as a center with the zenith distance of a second observation as a radius, an arc may be drawn which will intersect the first arc at the position of the vessel. The run between the sights will, of course, require the first arc to be carried forward as the first position line in the ordinary double altitude problem.
Johnson’s Method
It is not always found convenient to plot the position lines of a set of observations on a chart; perhaps for lack of a chart of proper scale or possibly for want of the chart itself. Again many navigators do not take kindly to the graphic method, but prefer to solve their latitudes or longitudes by computation. In any event Johnson’s Method comes as a relief to such persons, saving them from the arduous duty of establishing a set of position lines by the chord method of assuming two latitudes to get two longitudes.
Johnson’s Method can be practiced in both the double altitude problem of the sun, where the first sight, or position line, is brought forward to the second sight by correcting it for the intervening run, or where stars are used simultaneously.
Chief among its merits is the saving of figures. It is only necessary to compute two (instead of four) chronometer [Pg 124] sights in order to find the ship’s position, thus obtaining a mathematically accurate result by a short cut. But also a great advantage in the Johnson Method is that the resulting longitude is obtained by calculation and it is not necessary to plot the lines upon the chart to secure the position.
In using Johnson’s method it is not absolutely necessary to observe two stars simultaneously as the quick work of a good man is sufficiently close for the practical purposes of navigation.
It becomes evident to anyone reading the foregoing pages that every ordinary time sight places the vessel on a circle of equal altitude, the longitude resulting from the computation, depending on the latitude, by dead reckoning, used. Now rather than work two sights employing two assumed latitudes on either side of the supposed position, make the calculation only once, using the latitude by account.
Suppose by way of explanation that the altitude of a star bearing S. 55° E. is observed simultaneously with that of another star bearing S. 25° E. The longitudes derived by working the time sight of each should be identical, provided the altitudes are the true altitudes, the Greenwich time is without error, and the latitude used is correct. A combination of accuracy, indeed, and one not likely to be experienced often in actual practice. However, a skillful navigator should find no great difficulty these days in always having the correct Greenwich time at hand. There is always, of course, an opportunity for the display of skill in measuring altitudes, refraction particularly being an illusive element and not always easy to detect. [Pg 125] But if care has been taken to eliminate the errors as much as possible from the time and the altitude, it is safe to consider any discrepancy between the resulting longitudes as accountable to an error in the dead reckoning latitude.
The method of obtaining the ship’s position from the difference in the longitudes, derived from double or simultaneous observations, was originated by A. C. Johnson, R. N., and its many advantages have for years made it the most popular form among progressive shipmasters. The working of this problem involves the application of a correction to each calculated longitude in such a way as to bring them into agreement. The tables (Bowditch Tables 47 and 48) furnish this correction, which is known as the longitude factor and is symbolized by the letter F. It constitutes the change in longitude due to a change of 1´ in latitude. This quantity changes directly with the change of azimuth of the body; for example, the change in longitude is nil if the change in latitude is made on a due north or south line, and change in longitude increases as the change in latitude is made on lines bearing more and more eastward or westward. So it is necessary in order to obtain these corrections to have the true azimuths of the bodies at the moment of observation to use as an argument in the table of longitude factors. These are readily taken from the Azimuth Tables or diagram using the data furnished by the time sight.
The two longitudes obtained from time sights in which the same dead reckoning latitude is used, lie on the parallel of this latitude, but (unless the two longitudes happen to be coincident) the ship’s position is either north or south of this parallel according to the error existing in the dead [Pg 126] reckoning latitude. If the observed azimuth of the body (or bodies) fall within the same quadrant or in opposite quadrants, the correct longitude will be found to the eastward or the westward of both calculated longitudes. This is clearly shown in Fig. 7; both azimuths are between south and east. If the observed azimuth of the body (or bodies) fall in adjacent quadrants say, one between south and east and the other between south and west, the ship’s position will be found between the two calculated or erroneous longitudes. The position of this true longitude is determined by means of the before-mentioned factors. The factor of a longitude is the distance of the true longitude east or west of the meridian passing through the calculated or erroneous longitude, assuming the latitude to be in error 1´. The moment of this factor, it will be seen, depends on the azimuth of the body, which in turn determines the direction of the position line.
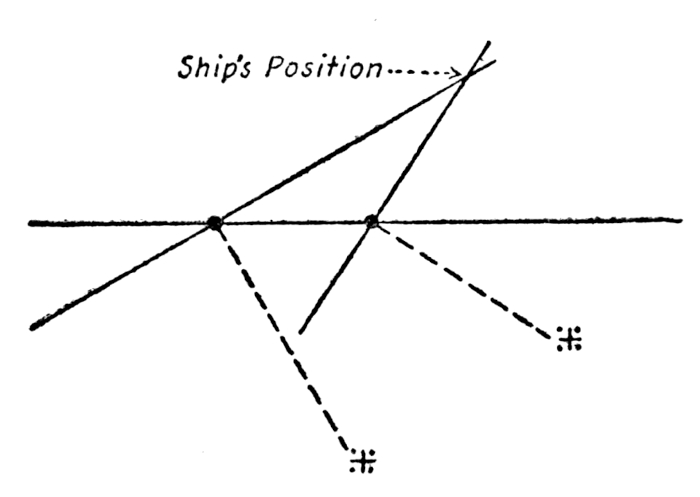
Fig. 7.
The combination of the two factors, by adding if the bodies are in the same or opposite quadrants or vice versa, is the combined error in difference of longitude due to 1´ of error in latitude. It now becomes a matter [Pg 127] of proportion by which to obtain the error in the dead-reckoning latitude. As the combined error in difference of longitude for 1´ of latitude, is to 1´ of latitude, so is the difference between the two calculated longitudes, to the error in latitude.
The longitude factors are based upon an error of 1´, so if the error is more than 1´ it becomes necessary to multiply the factor by the error in order to obtain the correction to the calculated or erroneous longitude.
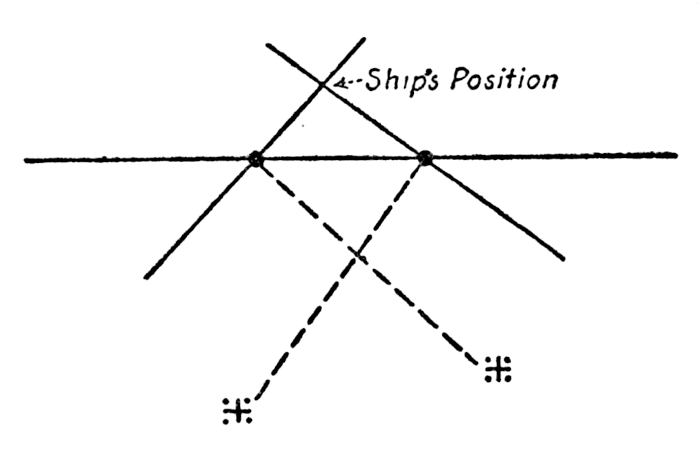
Fig. 8.
An altitude may be taken of any body and after a suitable change in bearing has taken place (not less than 30°) a second altitude may be taken and the first longitude advanced for the run during the interval to the parallel of the latitude by dead reckoning at the time of second sight.
In the usual event of a disagreement in the calculated longitudes the rule of procedure is as follows: With the body’s true azimuth at each observation, the difference between the longitudes and the latitude by dead reckoning, used at second sight, enter Table 47, Bowditch, and take out the corresponding numbers. If the azimuths are in adjacent quadrants, these quantities should be added, but [Pg 128] if in the same or opposite quadrants, they must be subtracted. The result in each case gives the combined error in difference of longitude for an error of 1´ in latitude.
It is now only necessary to divide the difference between the two longitudes by this combined error and we have the error between the correct latitude and the latitude by dead reckoning. Now multiply the error in latitude by the number taken from Table 47 corresponding to the first longitude, to obtain the correction to that longitude, and by multiplying the same error in latitude by the number corresponding to the second longitude we have the correction for that longitude. The application of these corrections should bring the two calculated longitudes into agreement at the position of the true longitude.
Some difficulty may be experienced in learning how to apply these corrections to the calculated longitudes, but it is always easy to make a rough diagram if at all in doubt. A horizontal line representing the parallel of latitude by dead reckoning at second sight may be drawn with the two longitudes plotted upon it; establish the position lines through these longitudes by drawing them at right angles to the sun’s (or star’s) azimuth. The intersection of the two position lines indicates the true longitude and a glance shows how to apply the corrections to each calculated longitude to get the true. In Fig. 8 the westerly longitude requires the correction to be applied to the east and the easterly longitude correction to the west in order to arrive at the true longitude.
Without the use of a diagram a rule easy to remember in deciding whether to apply the correction in longitude to [Pg 129] the eastward or westward is here given: If the error in latitude is of the same name as the first letter of the bearing, the change in longitude is contrary in name to that of the second letter and vice versa. For example take the case just cited.
When a body’s azimuth is less than 45°, it is wiser, and insures more accurate results to work by New Navigation, or, if sufficiently close to the meridian, as an ex-meridian. In the case of the latter the corrections in such a case are taken from the table of latitude factors (Bowditch, Table 48), the problem being the same in principle and in solution as that described above. Good results are even obtained by using two ex-meridians, one on each side of the meridian. The corrections in the latitude may be applied according to the following rule, if it is preferred to the rough diagram method: if the error of longitude is of the same name as the second letter of the bearing, the change in latitude is of the contrary name to the first letter, and vice versa.
The New Navigation
In every branch of science and industry since time immemorial a continuous process of simplification and increased accuracy has been taking place, and amid this general evolution of working systems the science of navigation will not be found an exception. Even now there is a tendency to displace the time-honored chronometer sight, together with a long list of more or less bewildering ways of obtaining latitude and longitude.
The advance method is popularly known as the New Navigation, yet its principles were originally brought forward [Pg 130] by Marcq St. Hilaire, a French admiral, nearly 40 years ago. It is not a new method of finding position, but rather an improved way of establishing a Sumner line. Like many innovations it has taken all these years for navigators to become reconciled to the change and break away from the more familiar forms.
In order to facilitate a simple explanation of New Navigation it will be brought to mind that every heavenly body has a corresponding point on the earth directly beneath it, which bears the same relation in latitude and longitude to the earth, that the body does in declination and right ascension to the celestial sphere. To an observer at such a sub-celestial point the body is in the zenith with an altitude of 90°; and about him lies a system of concentric circles of equal altitude, which extends over a hemisphere of the earth 90° in every direction from the point of origin. This point, through the apparent diurnal revolution of the body, carries this whole system of circles around the earth each day and northward and southward with the body’s change in declination. On the outer limit of this system of circles, the altitude of the body is 0°. Thus it is seen that the altitude of the body decreases and its zenith distance (90° - altitude) correspondingly increases in direct proportion as the observer departs from the sub-celestial point, and vice versa. If, for instance, an observer is 100 miles (nautical) from this point, the zenith distance is 100´ or 1° 40´ and the altitude of the body is 88° 20´; at 2700 miles 2700´/60 = 45° of zenith distance, and 90° - 45° of altitude.
A feature is now introduced that has a close bearing upon [Pg 131] the principle under discussion, to serve as an opening view of the subject: A navigator fortunate enough to have a body reasonably near his zenith, say 5°, has at hand an extremely simple way of graphically finding his ship’s position. This situation has previously been described, but is repeated to make clear the principle of New Navigation. The sub-celestial position of the body at the moment of observation is readily ascertained by noting the time by chronometer and recourse to the Nautical Almanac for its declination. With the point thus established as a center, and the zenith distance derived from the observed altitude as a radius, swing a circle upon the chart. The ship’s position is somewhere on the circumference of this circle of equal altitudes. This circle is now carried forward the amount and direction of the run of the vessel between this observation and a subsequent one similarly taken. During this interval the bearing of the body should have changed sufficiently to make a good intersection of the circles. The ship being on both circles must be at one of the two intersections, between which the mariner can readily decide. The conditions cited are comparatively unusual but show the practical use of a circle of equal altitude in its simplest form.
The zenith distance is ordinarily too large to become a radius for such use on the chart. The circles of equal altitude are in practice so large that 10 to 40 mile arcs in the vicinity of the vessel are treated by her navigator as straight lines, known as Sumner or position lines. These lines are, theoretically, chords or tangents according to the method employed in establishing the line, but in practice the divergence from the circle is negligible, excepting always [Pg 132] when the body is too close to the zenith. The establishment of the position line has been done in several ways for many years until the advent of this new and more expeditious method.
The altitude of a body at any selected time for an assumed position can be readily calculated. If this altitude does not agree (and it seldom does) with the altitude measured simultaneously with the sextant, corrected for the usual errors, the assumed position is not coincident with the actual position of the vessel. The navigator now proceeds to lay off from the assumed position, the line of azimuth of the body taken from the azimuth tables, Weir’s Azimuth Diagram, or determined by observation. On this line the distance between the observed and computed altitude, expressed in minutes of arc, is measured, towards the body if the observed altitude is greater, and away from it if less, than the computed altitude. The point thus indicated is a position on a circle of equal altitudes, the arc in the immediate vicinity of the computed point being, approximately, the position line. This line is at right angles to the azimuth for the reason that a tangent is at right angles to the radius of a circle at a given point.
It is now known that the ship is somewhere on this line of position, and it is necessary to cut it with another such line to determine definitely her position. If the sun is the body being observed, it becomes necessary, in order to provide a good angle of intersection, to wait until the azimuth changes at least 30°, when the observation is repeated, a second line established, and the first line brought forward in exact accordance with the ship’s run. The interval required naturally depends upon the latitude [Pg 133] of the ship and the declination of the sun. The intersection of the lines will be the position of the ship at the time of the second sight.
The use of stars has a decided advantage in that there are always some of these bodies available for observation lying in various azimuths; it is practicable, with a well-defined horizon, to observe simultaneously two or more of these bodies whose bearings show that they would produce desirable position lines. From the resulting intersections the position of the ship is secured. This obviates waiting for the second line, a feature that is always inconvenient and sometimes, perhaps, dangerous.
The calculation of the altitude is accomplished by the solution of the spherical triangle in which we have given the co-latitude (90° - assumed latitude), the polar distance and the hour angle of the meridian of the assumed position. Thus with two sides and the included angle, the third side or the zenith distance (90° - altitude) is easily determined by either of several formulas.
With the use of this method all the formulas that formerly, and still, often puzzle the navigator to remember can be reduced to this one sight. One of the most important features it possesses is that it can be utilized regardless of the altitude of the body (except when very high), its azimuth, or its hour angle, all of which are elements that have to be used under certain favorable circumstances in order to get accurate results from the older forms. The navigator is now given a greater freedom in choosing bodies to observe than is found in any other method.
The mariner to-day has been almost entirely relieved [Pg 134] from the labor of computing position at sea, should he care to avail himself of a set of altitude tables, several excellent ones have made their appearance on the market, among them Hydrographic Office Publication No. 200. From them the altitude can be selected corresponding to the conditions of any particular observation. With a set of these tables a navigator is no longer required to be a mathematician or to remember the forms of a half dozen sights. Thus in this wonderful age the mariner’s utopian dream of obtaining position at sea by inspection, is, in a way, realized.
In order to illustrate the practical working of a problem by this method, the following example is taken up point by point:
Early on the morning of May 21, 1899, while in the assumed position of latitude 55° 00´ N., longitude 112° 08´ E. observed the true altitude of the star Arcturus to be 37° 14´ 50´´, bearing west of the meridian. The chronometer carrying Greenwich mean time read 20 d. 6 h. 20 m. 03 s. The observer desired his position.
The problem by the St. Hilaire method resolves itself into the solution of the spherical triangle shown in Fig. 10, where two sides and an included angle are given:
Polar distance = 90° - declination (Nautical Almanac).
Co-latitude = 90° - latitude (by dead reckoning).
Hour angle of star. See figure and solution below.
The hour angle of the sun is more readily found than that of a star. It is accomplished by applying the longitude (in time) of the assumed position to the Greenwich time shown by the chronometer at the time of sight. This [Pg 135] hour angle of the mean sun must be corrected by the equation of time to obtain the hour angle of the actual sun.

Fig. 9.
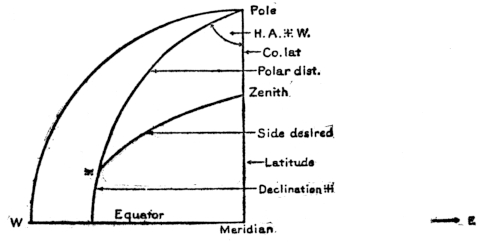
Fig. 10.
[Pg 136] The cosine-haversine formula serves the purposes of this problem very satisfactorily:
Hav z = hav (L~d) + cos L cos d hav h
which is derived from the well-known expression:
Cos z = sin L sin d + cos L cos d cos h
where z = zenith distance; L = the latitude; and h = the hour angle.
Solution
| Dec. Arcturus 19° 42´ 29´´. | |||||
| Lat. 55° 00 N. (Assumed). | G. M. T. | 20 d. | 6 h. | 20 m. | 03 s. |
| R. A. M. ⊙︎ | 3 | 51 | 42 | ||
| Acceleration | 1 | 02 | |||
| Lat. 55° 00´ 00´´. | G. S. T. | 10 | 12 | 47 | |
| Dec. 19 42 29 | Long. | 7 | 28 | 32 | |
| —————— | |||||
| L~d 35 17 31 | L. S. T. | 17 | 41 | 19 | |
| R. A. ⁜ | 14 | 11 | 03 | ||
| H. A. ⁜ | 3 | 30 | 16 W. | ||
| (Observer) | 52 | 34 | 00 | ||
| Lat. | 55° | 00´ | 00´´ | = cos. | 9.75859 | ||
| Dec. | 19 | 42 | 29 | = cos. | 9.97378 | ||
| H. A. ⁜ | 52 | 34 | 00 | = hav. | 9.29244 | ||
| 9.02481 = nat. hav. | .10588 | ||||||
| nat. hav. 35° 17´ 31´´ | .09189 | ||||||
| z = 52° 48´ 35´´ | = nat. hav. | .19777 | |||||
| 90 00 00 | |||||||
| Computed altitude | 37 11 25 | ||||||
| Observed altitude | 37 14 50 | ||||||
| Altitude difference = | 3´ 25´´. | ||||||

Fig. 11.
A ship’s position is usually obtained by plotting the lines of azimuth and the position lines much in the manner shown in the chartlet. The azimuth of the body at the moment of observation is readily taken by inspection from the azimuth tables or better still from Weir’s Azimuth [Pg 138] Diagram, both published by the U. S. Hydrographic Office.
In order to get an intersection of two lines of position and thereby ascertain the latitude and longitude at once it is assumed that the observer took an observation of another star bearing S. 45° E., simultaneously with Arcturus.
When ordinary A.M. time sights are taken the resulting longitude establishes a north and south Sumner line but the latitude is by D. R.; at noon the latitude by meridian altitude establishes an east and west line but the longitude is by D. R. So it is with a Sumner line a position is established upon it but the position along it is by D. R. The latitude and longitude, however, can be obtained by a slight calculation without drawing the lines on the chart; that is, the most probable position. The altitude difference having been determined enter Table 2, Bowditch, using the azimuth, or its reciprocal as the case may be, as the course, and with the altitude difference as the distance, pick out the difference of latitude and the departure and apply them to the dead reckoning latitude and longitude as is the usual practice. The result is the most probable position (according to the D. R.) on the Sumner line.
The moon is the most interesting of the heavenly bodies not only from a romantic viewpoint, but from the astronomical as well. Looking at the practical side, it is due mostly to the moon’s influence of attraction on the waters of the earth that we have the highly important phenomena of the tides. The moon is our nearest neighbor in the heavens; in fact, she is a satellite, that is, revolves around the earth. This movement is from west to east at an average rate of 51 minutes each day. The moon’s orbit is elliptical with the earth lying a little out of center, not unlike the situation of the sun in the earth’s orbital ellipse but more pronounced. When the moon is at the nearest point to the earth she is said to be at “perigee” and the point where she is most remote is called the “apogee.”
The moon is a non-luminous body and gives off nothing but reflected sunlight. The lunar hemisphere facing the sun is therefore the only illuminated portion of the body, and as she turns on her axis precisely as the earth does, the same side is always towards us. The astronomers have seen but one side of our satellite. This solar illumination accounts for the various interesting phases of the moon which we see each month. When this body in her monthly revolution around the earth passes between us and the sun, the illuminated side is towards the sun and the dark [Pg 140] side towards us. We see no moon at this time and call it New Moon. Two weeks later, she has completed one-half of her revolution and is now on the other side of the earth and we are between the moon and the sun. The illuminated face of the moon is now directly towards us and we call it Full Moon. At the time of new moon, the eastward movement quickly brings her out of range with the sun and in a couple of days we are able to see a fine crescent in the western sky. This is the very edge of the illuminated face—we can see around the corner just that much. Day after day the moon’s lighted surface becomes larger and larger until in about a week she is near our meridian at sunset and therefore at, roughly (depending on the time of the year), 90° from the bearing of the sun. The moon now presents to us a face one-half dark and one-half light. This is called the quadrature. This term also applies to the similar condition occurring a week after full moon when she is again bearing at right angles to the sun. These occasions are also called the first and last quarter, respectively.
The movements of the moon are very rapid. She makes her revolution around the earth in 27⅓ days, making a change in right ascension of 360° or 24 hours in this interval, a change of over two minutes each hour. The declination passes through its whole cycle of change from north to south and return also in 27⅓ days; the sun requires a year to pass through its extremes of declination and return. The change of the moon’s declination averages about 9´ per hour. These facts demand careful attention when employing the moon in navigation.
It is a very curious and happy circumstance that in the [Pg 141] higher latitudes when the short days of the winter sun occur, the moon at full rides its highest declinations, and consequently gives extra long nights of moonlight; and that in the summer, when the sun is in higher declination and the days are long, the moon at full is in low declination and there is less moonlight when it is least needed. The reason of these conditions is that the full moon occurs when on the opposite side of the earth from the sun and at the winter solstice when the earth’s north pole is inclined away from the sun she must be inclined towards the moon passing that body in high declination. The reverse conditions exist at the summer solstice.
Another fortunate provision for lovers of moonlight nights is the fact that the plane of the moon’s orbit is not in the same plane as that of the earth’s orbit, for if such were the case each time the three bodies, the earth, sun and moon, came in range there would be an eclipse. The new moon coming in between the earth and the sun would cause an eclipse of the sun, and at full moon when the earth is between the sun and moon, there would be an eclipse of the moon. Therefore, there would be an eclipse twice a month. This fortunately is avoided by the angle of 5° that the plane of the moon’s orbit takes with that of the earth. As a result they only come in exact range occasionally when the moon at new and full happens to be on the ecliptic—the earth’s orbit. If, to repeat, this occurs at Full there is an eclipse of the moon, if it occurs at New, there is an eclipse of the sun. The moon moves eastward through the heavens on her monthly course of revolution; it then becomes apparent that she must return to the meridian later and later each day the amount of “retardation,” [Pg 142] as it is called. This retardation is a variable quantity dependent upon the moon’s irregular change in right ascension. It is caused by the moon’s motion in her elliptical orbit and at the inclination which her orbit takes with the celestial equator. These causes are precisely the same in character as those producing the equation of time in the conditions relative to the sun and the earth’s orbit, but those of the moon are much greater. The errors causing a variation in the right ascension of the sun requiring a year where the similar conditions in the moon are brought about in a month, which accounts for the marked changes in the moon’s rate of eastward motion. The average daily retardation, or average later time in arriving at the meridian, is very close to 51 minutes. Yet the extremes of retardation range from 38 to 66 minutes. The average of 51 minutes daily retardation is also noticed in the later rising and setting of the moon. The extreme times between successive risings or settings during the year, while they average 51 minutes like the crossing of the meridian, they do not maintain the same extremes, changing on account of the latitude of the observer as well as upon her own motions. At 41° north the retardation on successive risings and settings ranges between 23 minutes and 1 hour and 17 minutes. As the vessel proceeds farther north the range is greater until near 66° north when the moon is in her average greatest declination north she does not set at all becoming circumpolar for a certain time each month. In the duration of a month the moon changes her right ascension 24 hours, where the sun takes a year to accomplish this amount as it (apparently for navigational purposes) moves eastward around the earth. [Pg 143] This shows the much more rapidly increasing change in right ascension in the case of our satellite. Thus again the moon’s rapid motions are accounted for.
The moon’s orbit around the earth is not coincident—does not lie in the same plane as the earth’s orbit (the ecliptic) but takes an angle of about 5° 8´ with it. The point of intersection between the moon’s orbit and the ecliptic are called nodes (corresponding with the equinoxes). The point crossed by the moon as it passes from southern to the northern side of the ecliptic is called the ascending and the other the descending node. The moon’s axis is very slowly describing a circle in the heavens similar to that of the earth; and in consequence the nodes are slowly moving westward along the ecliptic year by year. Just as is the equinox by the movement of precession, but at a much greater rate (see remarks on precession elsewhere). The moon’s axis completes its revolution in about 19 years, while the earth requires 26,000 years. This is called the lunar cycle. At the time in the lunar cycle when the ascending node of the moon’s orbit is in range with the vernal equinox the moon has her greatest range of declination—about 57° from extreme north to extreme south. She is then 23° north, the amount that the ecliptic is from the equator and 5° more, the amount that the moon’s orbit is above the ecliptic. About 9½ years later when the moon’s axis has listed in the opposite direction and the descending node coincides with the vernal equinox, the moon’s maximum declination equals 23° minus 5° or 18° north or south, a range of only about 26°.
[Pg 144]
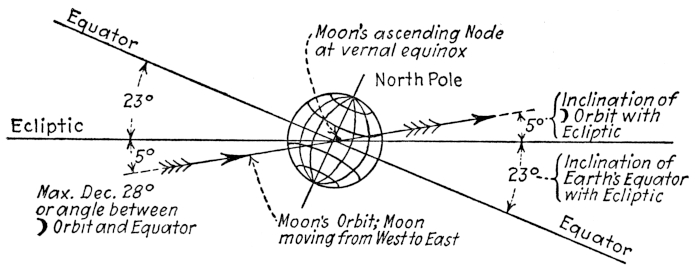
This figure is viewed from the sun looking towards the earth on March 21st—the vernal equinox.
Fig. 12.
In the autumn, there occurs an interesting phenomenon regarding the moon called the Harvest Moon. This is [Pg 145] the time of unusually fine moonlight nights in which the moon rises for three or four evenings at about the same time instead of the usual rapid retardation. The time the sun or moon is above our horizon depends upon its declination and our latitude. As the sun moves northward in declination from March to June, our days lengthen by the sun rising earlier and farther in the northeast, and setting later and farther to the northwest. Similarly the moon in September is moving northward in declination very rapidly and would be rising earlier each evening were it not for its own eastward movement of revolution which causes her to slip eastward an average of 51 minutes daily and causes her later rising at night. The result is that these two influences at work almost counteract each other and cause the moon to rise at about the same time for several days giving us three or four glorious moonlight nights called the Harvest Moon.
It will be seen by the foregoing that great care must be exercised in having the time of observation accurately determined owing to those rapid movements of the moon. It is also a matter of great difficulty to correct the observed altitude of this body on account of numerous errors that become considerable in amounts due to her proximity to the earth. And for these reasons this body is not popular for observations with the general run of navigators. In the case of the semi-diameter, considerable error is apparent and is fully described, with parallax, which is excessive, under “Corrections for Observed Altitudes.”
A difficulty was encountered when the early cartographers attempted to represent the earth’s spherical surface on a flat sheet. It can not be done, of course, without distortion being introduced in some manner. There are various methods of taking care of this error and one is adopted for one certain purpose while another scheme is used in some other work. These methods of caring for the error or distortion are known as projections, the principal being the Mercator, the gnomonic and polyconic. The Mercator projection is almost universally used for navigational purposes; the gnomonic projection facilitates the use of great circle sailing, and the polyconic is used for surveying sheets.
The Mercator chart represents the earth as though it were a cylinder instead of a sphere.
If we take the skin of one-half an orange, and assume it to represent the northern hemisphere of the earth, an attempt to forcibly bring it flat upon a table will result in the tearing or stretching of the skin. It can, however, be brought flat to the table in a regular uniform way by cutting it in a saw tooth fashion from the stem (pole) to the edge (equator), as shown in the diagram.
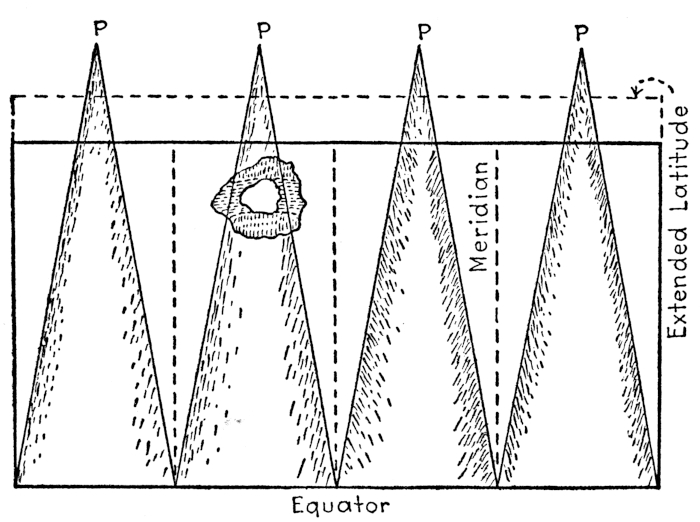
Fig. 13.
The shaded portions represent actual earth’s surface and the blank parts show the error introduced by using [Pg 147] this method. In this form it is useless as a chart, so the real parts are stretched or extended each way to the dotted lines making a complete chart. It is now, however, without a vestige of accuracy in representing the bodies of land and water as they really exist. The result would be that if a round island should be in the latitude of the top of the chart it would be stretched into an elongated island lying east and west giving a very erroneous inaccurate idea of it, as shown by the east and west shading. If, however, the island had been on the equator where no east and west stretching would have occurred the island would appear in its natural shape, but the farther north or south it lies just in proportion to the latitude will it be stretched in an east and west direction. Such a condition will not serve [Pg 148] the purposes of navigation and it becomes necessary to extend the degrees of latitude, making them appear longer and longer as the equator is departed from. This stretches the elongated east and west island in a north and south direction and brings it back approximately to its actual shape of a round island. If there was a round island in 10° N. and a similar-sized similar-shaped island in 50° N. the Mercator chart would show the northern one to be almost twice as large owing to this artificial distortion. But its relative shape would remain practically correct. It will be seen that the latitude scale on the sides of the chart carries an increasing value towards the north—on a chart where a degree is about ¼´´ long at the equator it would be about ½´´ long in 60° N. or S.
A minute of latitude is equal to a mile on this scale, but it becomes necessary to use it in the latitude in which the measurement is taken. If a course runs N. 60° E. from latitude 30° N. to 40° N. and the distance is desired, take at the middle latitude at the side of the chart a convenient multiple of distance, say 30´, on the dividers and step off the distance. Or the whole course can be taken off at once and with the points of the dividers at equal distances north and south of the middle latitude read off the number of minutes of latitude lying between them.
In very high latitudes the Mercator chart is not reliable. The distortion becomes excessive and bearings taken will not plot correctly.
All the meridians on a Mercator chart are parallel and cut the equator at right angles. They all lie in a true north and south direction. The parallels of latitude all lie east and west and are parallel to each other and at right [Pg 149] angles to the meridians. The degrees of longitude on the globe grow smaller and smaller as the pole is approached due to the actual convergence of the meridians, but as all meridians are parallel on the Mercator chart the length of a degree must be shown the same length at the top as well as at the bottom of the chart. In just the proportion that the degrees of longitude have been lengthened artificially beyond their true length must the degrees of latitude be lengthened in each latitude. This amount is shown in Table 3, Bowditch, reckoned as the distance in miles each parallel is from the equator by the Mercator projection. Thus in latitude 40° N. the distance is 2400´ or miles, the table shows that in the construction of a Mercator chart this parallel should be increased artificially to 2607.6. These are called the meridional parts.
On a Mercator chart the ship’s course is represented by a straight line and cuts each meridian at the same angle and is called a rhumb line. For all practical purposes on short runs this rhumb line is the best to use, but it is not the shortest distance between two points. Should you be able in a course a thousand miles long, to see your port of destination your rhumb line course at the outset would not head your ship for it, but (in northern latitude) to the southward of it. However, as you proceeded the ship’s head would gradually draw towards the port and you would eventually arrive. What appears to be a straight line on this chart is really a curve on the sphere of the earth. Your line of actual vision is a great circle, and in order to follow such a bee line you must constantly change your compass course (on a long run) and describe a curve on the Mercator chart unless the ship is headed north or south or east or [Pg 150] west along the equator, in which cases she is sailing on a great circle. The well-known Hydrographic Office Pilot Charts are on the Mercator projection and show all steamship tracks as curves, for they are great circles.
The gnomonic chart is based on a projection of the earth’s surface upon a plane tangent to any chosen point which is to be the center of the chart. The eye is assumed to be at the center of the earth looking outward to the point of tangency. It will be seen that the surface of the earth adjacent to the point of tangency will be very accurately shown on the chart, but becomes distorted gradually from the center, the sides of which show the land in such an unnatural shape that it is hardly recognizable.
With a chart on this projection great circle sailing is much simplified. The straight line between two points indicates the great circle to follow, and the course and distance is obtained by following the directions and illustrated example given on each chart. They are constructed for the different oceans and are for sale by the Hydrographic Office.
The course can be transferred to a Mercator chart by taking successive positions from the gnomonic chart and plotting them according to latitude and longitude, and joining by straight or curved lines.
In setting out on a voyage the port of destination could it be seen ahead would indicate the great circle course, and in order to continue to head directly for it, the course must be continually changed. While in the North Atlantic bound for Europe the course must be changed constantly to the east (right) in order to remain [Pg 151] on the great circle—the straight and shortest distance.
The course and distance can be computed by the form given in Bowditch, in which two sides and an included angle are given to find the other side and the (course) angle at the point of departure. The co-latitudes of the points of departure and destination and the angle between them at the pole, are respectively the sides and the included angle. However, the gnomonic chart gives the course and distance graphically.
When a chart is purchased or received from the Government offices the date of issue stamped upon it should be carefully noted. It can safely be taken for granted that the chart has been corrected up to that date and it is incumbent upon the navigator or master to seek in all Notices to Mariners subsequent to this date for any that affect the chart. If a Notice contains information requiring a correction the number of the chart appears in boldface type. The alterations should be made neatly with India waterproof ink, and if by the nature of the information it is impracticable to make the changes a note should be made in a conspicuous place.
Charts are printed from copper, zinc or aluminum plates and small changes easily made by hand are not changed on the plate until an accumulation of errata make it necessary, or sweeping changes of a more extensive nature takes place such as a new survey, dredged channels, etc. A chart under extensive correction is brought up to date in every particular, including the latest geographic spelling, [Pg 152] new docks and public works. The date is noted on the right of the center margin and the dates of smaller hand corrections are indicated at the lower left corner; the figures denote the number of the weekly Notice to Mariners, in which the information is found, and the year.
The different scales of charts range from those of the world to a harbor plan. There are charts of oceans; general coasts, such as from the St. Lawrence to below New York; intermediate coasts, as from Eastport, Maine to Cape Ann; and approaches to ports, say from Cape Ann to Cape Cod for the port of Boston; and lastly there are harbor plans. Those covering large areas are known as small-scale charts while harbor charts are called large-scale charts.
A chart depends on the surveys that furnished its data, and its accuracy and reliability rests upon that survey. Even with the most careful surveys, where the lead is used to ascertain depths, there are many instances where pinnacle rocks have escaped detection by coming between the casts of the lead taken by the surveying party. These isolated rocks become points of great danger to vessels of deep draft, and it becomes a measure of safety to avoid rocky coasts and offshore patches by giving them a wide berth. Spaces devoid of soundings may well be viewed with suspicion if in reasonably shallow water, for it would appear to indicate a lack of thoroughness in the survey, at least a lack of soundings. The wire drag, a device used to sweep important areas to a certain depth, is the only sure way of discovering all the dangers of the bottom.
The aids to navigation shown on the charts are described by symbols and abbreviations as fully as possible [Pg 153] with the limited space. All symbols are placed in the location of the aid, but in some cases the actual position may be in doubt by the nature of the symbol, for instance a buoy’s location is denoted by the ring that accompanies the symbol and not the triangle; a light vessel by the position of the dot of the light, or between them if there are two dots (lights). Buoys and light vessels often drag their moorings or go adrift entirely, especially in the winter season. It is therefore the part of wisdom to check a ship’s position by shore marks when possible and be prepared to find buoys out of position. The mechanism of a light buoy is often disarranged through various causes.
The characteristics of all lights are briefly given with the visibility and height above the sea. The charted visibility is the distance they should be seen from a vessel’s deck on which the height of the eye is fifteen feet above the sea, so, from the deck of an ordinary power boat a light will not be seen until well within the range of visibility as published, while from the deck of a large steamer the light will be seen outside its charted visibility. This refers to high-powered lights where the curvature of the earth has to be given consideration. A flashing light is one in which the flash is of less duration than the eclipse, while an occulting light has an eclipse equal to or less than the period of light. Flashes and eclipses are often grouped and receive the name of group flashing or group occulting. An alternating light is one in which two colors are shown each for an equal interval with no intervening eclipse, but if an eclipse separates the color flash from a white flash, for instance, it becomes a flashing white light varied by a red flash. It is a very common practice to insert sectors of [Pg 154] different colors into the arc of visibility of a light in order to cover a dangerous shoal or to indicate a channel. Bearings defining these sectors are taken from seaward and not from the light. The term luminous range will be met with, and indicates the distance the power of the light can carry the visibility irrespective of an intervening horizon. A light may have a luminous range much in excess of its visibility which is limited by the horizon but in a haze or fog its penetrating power will greatly exceed that of a light of similar visibility but less luminous range. The power of a light is more commonly shown by units of a thousand candle power, thus, 5.6 indicates a power of fifty-six hundred candles. The catoptric (C.) light employs the reflecting, and the dioptric (D.) the refracting principle.
There is a large amount of useful information given on every chart that the average mariner allows to escape his notice. This failure on his part is mostly due to familiarity, or reliance on pilots with local knowledge.
The first important feature of a chart to be considered is the shoreline, which is shown as a continuous line representing the high-water mark. This, it must be borne in mind, is much changed at low water, and where the range of tide is large the shoreline is proportionately in error. Again, where the water is shallow the change is more marked than where the shores are steep-to. If account is not taken of the stage of the tide it is easy to be very much deceived.
In approaching a strange harbor the chart should be scrutinized for prominent marks, and these identified as soon as possible, then the lesser objects can be picked up by their relative positions with the already identified landmarks. [Pg 155] Among the lesser marks may be found cliffs, boulders, sandy beaches, vegetation, buildings (particularly church spires and houses with cupolas). Prominent elevations of land always serve to identify a locality. The chart shows these elevations clearly by contour lines.
A twenty-foot contour line, for instance, shows the line of the cut, should the hill be sawed off twenty feet above the sea. When contour lines are wide apart the land has a gradual slope, and as the grade becomes steeper the contour lines come closer proportionately.
The chart, wherever possible, represents the earth as seen from overhead, but in the case of vertical objects, they are of necessity shown horizontally. One of the notable cases of this is in the representation of cliffs, which in order to show their height are drawn with the side view as seen from the water.
Numbers seen on the land show the height above the high water.
From the topographical features of a chart we turn to those of hydrography. All the depths indicated on a chart are those existing at mean low water, on the Atlantic Coast, and mean lower low water on the Pacific Coast.
All the British Admiralty and most of the Hydrographic Office charts are reduced to the level of low water at ordinary spring tides. While there is usually more water to be expected than shown, it must be remembered that when the plane of mean low water is used, the low waters that, roughly speaking, come between the moon’s first and last quarters, will fall below the soundings on the charts.
[Pg 156]
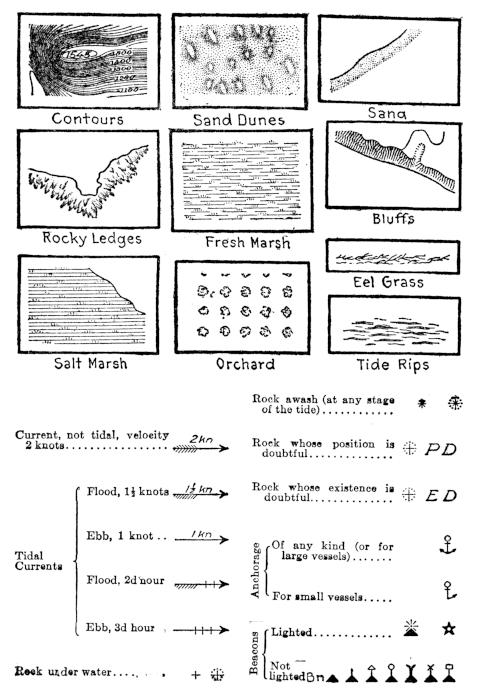
[Pg 157]
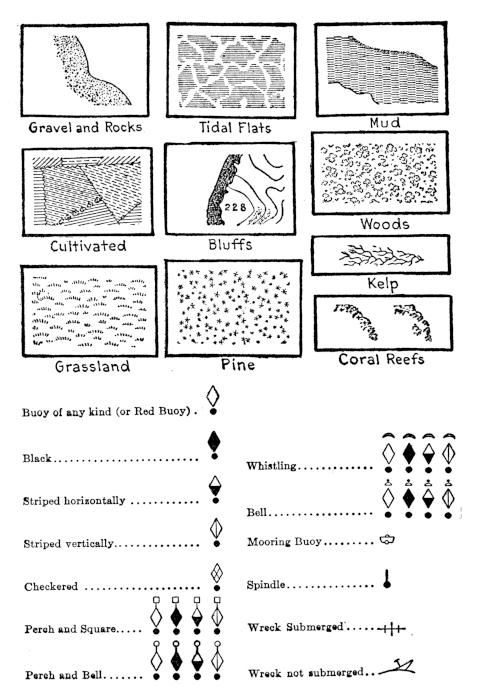
[Pg 158] The effect of an abnormal barometer and high winds must at times be borne in mind, for a continuous northwest wind will make a vital difference in the depths along the Atlantic seaboard, especially in the Delaware and Chesapeake Bays.
Very often there is information that can not be symbolized on the chart and is placed in italics in the form of a note. These are always important and should be read carefully.
Sailing directions are written to supplement the charts and preserve for the mariner a mass of information which otherwise would not reach him.
It is always well to pay attention to the current arrows, as they are a means by which the strength and direction of the tidal stream may be ascertained. The symbol of a tide rip should not be ignored by one in a small boat, as the conditions might be right to make them dangerous.
On the water areas of the chart we find contours of depths as on the land are contours of height. It is a good scheme, if one wanted to take the trouble to run a contour line indicating a depth a few feet greater than the draft of his boat, and tint the shallow water with a brush.
Large vessels of deep draft upon approaching the coast are guided by the ten-fathom curve unless the shore is very steep-to and the water very deep. The masters of such vessels would remain outside that curve until their position was well established. Lighter draft vessels are guided by the five-fathom curve in a similar manner.
When approaching the land and the landmarks are not available, the character of the bottom further assists the mariner as he sounds slowly towards the land. The kind [Pg 159] of bottom is indicated by abbreviations which are obvious on almost every portion of the charts.
The three-fathom curve is the most important to the greatest number of navigators and for this reason is made the most pronounced. In the majority of charts it is shown by a “sanded” area within it, but in many new charts it is heavily tinted.
In changing from one chart to another while working in an unfamiliar locality, take especial note whether the soundings are in feet or fathoms.
It is an excellent practice when a vessel is brought to anchor and cross bearings taken, to estimate the radius of her swinging circle by adding the amount of chain out to the length of the vessel and with this describe a circle on the chart and note if there is any danger of tailing into shoal water at any quarter.
This has been a long voyage and I am glad to tie up and let the printers take charge. If any of my readers see places where I have stood into the shallow water of inaccuracy, I will be grateful for a passing hail that I may shift helm and get out with as little damage as possible.
THE LITERATURE of NAVAL
AND MARINE SCIENCE
On our shelves is the most complete stock of technical, industrial, engineering and scientific books in the United States. The technical literature of every branch of naval architecture, construction, ordnance, marine engineering, seamanship and navigation is well represented, as well as are the various other related subjects.
A large number of these we publish and for an ever increasing number we are the sole agents.

All Our Inquiries are Cheerfully and Carefully Answered and Complete Catalogs as well as Special Lists are Sent Free on Request :: ::
D. VAN NOSTRAND COMPANY
Publishers and Booksellers
25 PARK PLACE NEW YORK
VAN NOSTRAND’S NAUTICAL MANUALS
350 Pages 5 × 7½ Postpaid, $3.00
The Men on Deck
MASTER, MATES AND CREW
Their Duties and Responsibilities
A Manual for the American Merchant Service
By FELIX RIESENBERG
Commanding Schoolship Newport
New York State Nautical School
| MASTER | ⎫ | Concise statement of their duties and responsibilities and the laws under which they work and live |
| Chief MATE | ⎪ | |
| Second MATE | ⎪ | |
| Third MATE | ⎪ | |
| WATCH OFFICER | ⎪ | |
| Junior Officer | ⎬ | |
| Cadet | ⎪ | |
| Quartermaster | ⎪ | |
| Carpenter | ⎪ | |
| Boatswain | ⎪ | |
| Foremast Hands | ⎭ | |
| DISCIPLINE—on board ship | ||
| The Books of the Sea | ||
Points out the things the various members of the deck department of an ocean or Great Lakes steam vessel may reasonably be expected to know, and the things they may be required to do. The book does not pretend to tell HOW, but shows WHAT a modern American seaman ought to know, and to do.
VAN NOSTRAND’S NAVAL BOOKS
730 Pages 6¼ × 9¼ Postpaid $6.50
159 Full Page Plates 10 Color Plates
Modern Seamanship
By
Admiral Austin M. Knight, U.S.N.
SEVENTH EDITION
REVISED AND ENLARGED
CONTENTS—The Hull and Fittings of a Ship. Rope. Knotting and Splicing. Mechanical Appliances on Shipboard. Blocks and Tackles. Handling Heavy Weights. Compass. Log and Lead. Submarine Signals. Boats. Handling Boats in a Surf. Ground Tackle. Carrying Out Anchors. The Steering of Steamers. The Rules of the Road. Manoeuvering to Avoid Collision. Piloting. Handling a Steamer Alongside a Dock. Placing a Ship in a Dry Dock. Weather and the Laws of Storms. Handling Steamers in Heavy Weather. The Handling of Torpedo Vessels. Keeping Stations and Manoeuvering in Squadron. Towing. Rescuing the Crew of a Wreck. Man Overboard. Stranding. Hints for Junior Officers Doing Line Duty. Appendix.
The official text book at the U. S. Naval Academy and in use throughout the service. Describes the handling of all vessels, men-of-war, merchantmen, naval auxiliaries and small boats.
Words may have multiple spelling variations or inconsistent hyphenation in the text. These have been left unchanged unless indicated below. Obsolete and alternative spellings were left unchanged.
Obvious printing errors, such as duplicate words, backwards, upside down, or partially printed letters and punctuation, were corrected. Final stops missing at the end of sentences and abbreviations were added.
The following items were changed:
“access” to “excess”
“Manoeuvring” to “manoeuvering”
“effect” to “affect”